VASP from a Gaussian-type orbitals perspective

For those of you first coming into VASP from outside of solid-state physics, many will be familiar with performing calculations using atom-centered, localized Gaussian-type orbitals (GTOs) as a basis. You may, however, be unaware of using delocalized, plane waves (PW) as a basis. This article will provide a brief introduction to plane-wave calculations, specifically those performed in VASP, with a comparison to GTO calculations.

Introduction

In electronic structure calculations, GTO bases are typically used for molecules and plane waves for solid-state calculations. There are exceptions, most distinctly in surface and material science, but often these two branches stay separate. Though there are many differences introduced by the choice of basis and periodicity, there are more similarities between GTO and plane-wave calculations than may at first be apparent , largely differing only in the choice of terminology. They both use the same basic methods, e.g. Hartree-Fock , Density Functional Theory (DFT) , and use the same algorithms both electronic (e.g. RMM-DIIS) and structural (e.g., quasi-Newton optimization, conjugate gradient). This is because they are simply different basis sets for expressing the orbitals; the Hamiltonian remains the same , though it is diagonalised iteratively in VASP, compared to being explicitly calculated in GTO codes. Sometimes the same algorithm is used for seemingly very different problems, e.g., the Davidson algorithm is used in the form of blocked-Davidson for diagonalizing the Hamiltonian in VASP (i.e., electronic structure), while in GTO codes, it can be used to diagonalize the configuration interaction (CI) matrices (i.e., excited state calculations), such as the CI singles (CIS) matrix . In each case, the problem is an eigenvalue problem for large, real-symmetric, sparse matrices where only the first few eigenvalues and eigenvectors are of interest, i.e., orbitals and low-lying excited states .

Hartree-Fock

Assuming the Born-Oppenheimer approximation, the Hamiltonian $\hat{H}$ for electrons p and nuclei A takes the form :

$\hat{H} = \hat{T} + \hat{V}_{ne} + \hat{V}_{ee} + E_{nn}$

where $\hat{T}$ is the kinetic energy operator for the electrons:

$\hat{T} = - \frac{1}{2} \sum_{p} \nabla_p^2$ (atomic units, a.u.) $= - \frac{\hbar^2}{2m} \sum_{p} \nabla_p^2$ (SI units)

$\hat{V}_{ne}$ is the potential acting on the electrons due to the nuclei:

$\hat{V}_{ne} = \sum_{p, A} V_A (|r_p - R_A|) = \frac{Z_A}{|r_p - R_A|}$ (a.u.) $= \frac{1}{4 \pi \epsilon_0} \frac{Z_A e^2}{|r_p - R_A|}$ (SI)

where r_p and R_A are the electron and nuclear spatial coordinates, respectively.

$\hat{V}_{ee}$ is the electron-electron interaction (between electrons p and q, or 1 and 2, alternatively):

$\hat{V}_{ee} = \sum_{p \neq q} \frac{1}{|r_p - r_q|} = r_{12}^{-1}$ (a.u.) $= \frac{1}{4 \pi \epsilon_0} \sum_{p \neq q} \frac{e^2}{|r_p - r_q|}$ (SI)

and $E_{nn}$ is the classical nuclear interaction.

The Hartree-Fock energy is then the expectation value of this Hamiltonian for a single Slater determinant:

$E_{HF} = \frac{\langle \Psi| \hat{H} | \Psi\rangle}{\langle \Psi|\Psi \rangle} \equiv \langle \hat{H} \rangle = \langle \hat{T} \rangle + \int d^3r \, V_{ne}(r) n(r) + \langle \hat{V}_{ee} \rangle + E_{nuc}$

where n(r) is the electron density.

In the Hartree-Fock equations for a closed-shell ground state, the energy is expressed in terms of one-electron and two-electron integrals over spatial orbitals (in a.u.) in chemist's notation, physicist's notation, and matrix form, respectively over occupied states i, j:

$E_{HF} = 2\, \sum_i (i|h|i) + \sum_{i,j} [2 (ii|jj) - (ij|ij)] + E_{nuc} = 2\, \sum_i \langle i | h | i \rangle + \sum_{i,j} [2 \langle ij | ij \rangle - \langle ij | ji \rangle ] + E_{nuc} = 2\, \sum_i h_{ii} + \sum_{i,j} [2 J_{ij} - K_{ij} ] + E_{nuc}$

where $(i|h|i)$ are the one-electron terms about nucleus I:

$(i|h|i) = \langle i | h | i \rangle = h_{ii} = \int dr_1 \,\psi_{i}^*(r_1) (- \frac{1}{2} \nabla_{i}^2 - \sum_{i, I} \frac{Z_I}{|r_i - R_I|}) \psi_{i}(r_1) = \langle \hat{T} \rangle + \int d^3r \, V_{ne}(r) n(r)$

The two-electron $\langle \hat{V}_{ee} \rangle = \sum_{i,j} [2 J_{ij} - K_{ij} ]$ is expressed in terms of $(ii|jj)$ and $(ij|ji)$, the Coulomb J_ij and exchange K_ij terms, respectively:

$(ii|jj) = \langle ij|ij \rangle = J_{ij} = \int dr_1 dr_2 \, \psi_i^*(r_1) \psi_i(r_1) r_{12}^{-1} \psi_j^*(r_2) \psi_j(r_2)$ and $(ij|ji) = \langle ij|ji \rangle = K_{ij} = \int dr_1 dr_2 \, \psi_i^*(r_1) \psi_j(r_1) r_{12}^{-1} \psi_j^*(r_2) \psi_i(r_2)$

In the HF energy expression above, these integrals are over occupied molecular orbitals MO (or Bloch functions in solid-state). Expressing the orbital ψ in terms of the basis functions φ and expansion coefficients C_μi, where μ is the basis function:

$\psi_i = \sum_{\mu} C_{\mu i} \phi_{\mu}$,

the one-electron integrals becomes $(\mu|h|\nu)$ and the two-electron integrals become $(\mu\nu|\lambda\sigma)$, where μνλσ are basis functions. It is primarily in the evaluation of these integrals where the plane-wave and GTO approaches differ. A secondary difference is the use of pseudopotentials, which are important for plane-wave calculations but infrequent when using GTOs; they will be discussed in more detail below.

Kohn-Sham equations

Another key difference is that, in solid-state calculations, it is far more common to use DFT to express the exchange and correlation terms as a density functional, instead of Hartree-Fock (HF) and the post-HF methods (e.g., MP2, CCSD). The Kohn-Sham (KS) energy E_KS equation differs from the HF to include the exchange-correlation energy E_xc (in a.u.) :

$E_{KS} = \langle \hat{T} \rangle + \int d^3r \, \hat{V}_{ion}(r) n(r) + E_{H} + E_{xc} + E_{nn}$,

where $\hat{T} = \hat{T}_{s}$, $\hat{V}_{ion}(r) = \hat{V}_{ne}(r)$, and $E_{H}$ is the Hartree energy, also referred to as the Coulomb energy J_ab.

The corresponding Hamiltonian $\hat{H}_{KS}$ is therefore:

$\hat{H}_{KS} = \hat{T} + \hat{V}_{ion} + \hat{V}_{H} + \hat{V}_{xc} + E_{nn}$

where the exchange-correlation potential $\hat{V}_{xc}$:

$\hat{V}_{xc} = \frac{\delta E_{xc}[n]}{\delta n(r)}$

The integral evaluation of each of these terms will be discussed for the PW and GTO bases.

Periodic boundary conditions

Before tackling the integral evaluation, it is key to consider another common difference between plane-wave and GTO approaches. Typically, GTOs are used for non-periodic and plane waves for periodic systems. There are exceptions to this where only Gaussians are used in periodic systems , and where the two are combined, i.e., in the Gaussian Plane Waves (GPW) method . Periodic codes can also be used to model non-periodic systems through the use of a vacuum and a large unit cell. It is possible to mimic small unit cells with local basis sets in a cluster approximation. These approaches are typically used for systems that have periodic and local parts, e.g., molecules adsorbed on a surface.

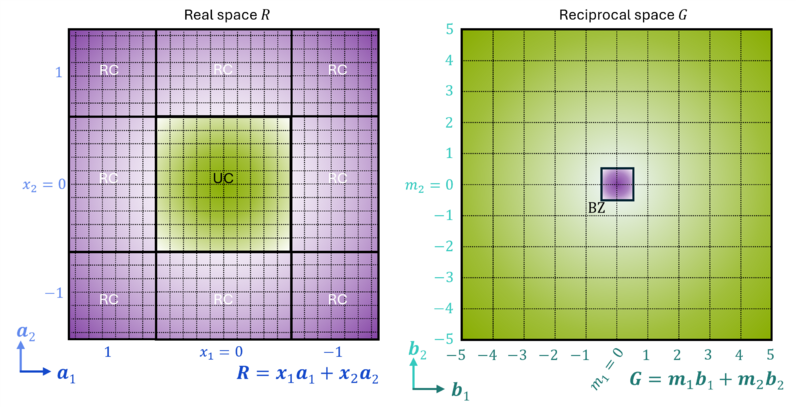
Returning to plane waves, Bloch's theorem states that , for electrons in a perfect crystal (i.e., Bravais lattice), a basis can be chosen such that the wavefunction is a product of a cell-periodic part u_nk(r) and a wavelike part e^ik⋅r :

$\psi_{n \textbf{k}}(\textbf{r}) = e^{i\textbf{k}\cdot\textbf{r}} u_{n \textbf{k}}(\textbf{r})$,

where $u_{n \textbf{k}}(\textbf{r} + \textbf{R}) = u_{n \textbf{k}}(\textbf{r})$; R is a translation vector in the Bravais lattice.

It can be alternatively expressed so that each eigenstates ψ is associated with a plane wave with wavevector k, such that:

$\psi_{n \textbf{k}}(\textbf{r} + \textbf{R}) = e^{i\textbf{k}\cdot\textbf{R}} \psi_{n \textbf{k}}(\textbf{r})$

Real space 11x11 grid inside the unit cell (UC) with repeating cells (RC) surrounding it. The corresponding grid in reciprocal space lies outside of the first Brillouin zone (BZ) (black square), except for at the Γ-point (center of the BZ). There is no one-to-one correspondence of points, each real space point is related to each reciprocal space point and vice versa. In reciprocal space, the contributions of distant RC are described within the BZ, while the contributions of the UC are described outside the BZ.

Plane waves

Since u_nk(r) has the same periodicity as the lattice, it can be expanded as a Fourier series (e.g., plane waves) in reciprocal (or k-) space :

$u_{n \textbf{k}}(\textbf{r}) = \sum_\textbf{G} c_{\textbf{G},n}(\textbf{k}) e^{i\textbf{G}\cdot\textbf{r}}$,

where G are the reciprocal lattice vectors and c_G,n(k) are Fourier coefficients.

The orbital ψ can then be expressed as a sum of plane waves:

$\psi_{n \textbf{k}}(\textbf{r}) = \sum_\textbf{G} c_{\textbf{G},n}(\textbf{k}) e^{i ( \textbf{G} + \textbf{k} ) \cdot\textbf{r}}$.

The orbital is evaluated over reciprocal (or momentum) space , where the entire periodic system may be efficiently described within a small part of reciprocal space, the first Brillouin zone (BZ). The BZ is uniquely defined such that everything in reciprocal space can be folded back into it. The whole of real space can be efficiently described within the BZ by integrating over it using a k-point grid. In general calculations, k-point integration means setting a KPOINTS file to describe the k-point mesh. These wavefunctions are those of the electronic bands, the band structure being the periodic analogue of molecular orbitals (MOs) seen in GTO calculations .

Plane waves are composed of sine and cosines. The three different plane waves in 1D (red, purple, and blue) sum to a regular pattern (Figure a). When this is Fourier transformed, each of these plane waves corresponds to a specific momentum (or kinetic energy), which is shown in reciprocal (or inverse) space (cf. X-ray diffraction patterns). The momentum associated with each plane wave corresponds to a point on the reciprocal space grid (see selecting the basis), and is therefore a vector. When many plane waves are used together (Figure b) and are separated in momenta using Fast Fourier Transformation (FFT), this spectrum becomes nearly continuous. Plane waves in VASP are used up to a cutoff, the energy cutoff, which excludes plane waves of high momentum (and therefore kinetic energy and frequency), shown in grey. Lots of plane waves are used to model the electronic structure, such as a crystal (Bravais) lattice. A 2D Bravais lattice modeled with plane waves transforms into a 2D reciprocal lattice of corresponding momenta (Figure c), each expressed as a vector. An equivalent step can be taken to 3D space, which is how the 3D electronic structure in crystals is modeled.

Atom-centered basis

In contrast to the delocalized plane-wave approach, in the atom-centered approach, the MOs ψ_i are expanded in terms of atomic basis functions ɸ_μ and corresponding expansion coefficients C_μi :

$\psi_i = \sum_{\mu = 1} C_{\mu i} \phi_{\mu}$.

Slater-type (exponential) functions or Gaussian-type functions can then be chosen. The advantage of Gaussian-type functions is that the electron integrals can be evaluated analytically. Using a Gaussian basis, the MOs can be expanded in terms of primitive Gaussians :

$\phi_{\mu}(\textbf{r},\alpha,\textbf{I}) = e^{-\alpha |\textbf{r}_\textbf{I}|^2}$,

where α is an exponent controlling the Gaussian's width, $\mathbf{r_I} = \mathbf{r} - \mathbf{I}$, r is the electron spatial coordinate, and I is the position of a nucleus I.

Usually, multiple primitive Gaussians are combined into a single function, known as a contracted Gaussian function $\phi^{CGF}_{\mu}$:

$\phi^{CGF}_{\mu} = \sum_j d_j \phi_{j \mu}$,

where d_i are contraction coefficients.

The MO can therefore be expressed in terms of contracted Gaussians as:

$\psi_i = \sum_{\mu} C_{\mu i} \phi_{i}^{CGF} = \sum_{\mu} C_{\mu i} \sum_j d_j e^{-\alpha_j |\mathbf{r_I}|^2}$.

analogous to the final equation in the periodic boundary conditions section, summing over contracted Gaussians rather than plane waves.

Integral evaluation

Any property of a system, whether molecular or crystalline, is usually expressed in terms of energy or a related derivative. Focusing on the energy, the equations given in the introduction require evaluation of one- and two-electron intervals. Evaluating these integrals is where Gaussian and plane-wave approaches significantly differ. We will first go through the recursion relations for generating the Gaussian integrals, before expressing the equivalent plane-wave integrals.

Mind: You do not need to fully understand the integral evaluation to compare the two approaches; the key message here is that evaluating integrals is much simpler using plane waves than GTOs.

Gaussian basis

Slater (exponential) functions more accurately model atomic orbitals, but the resulting electron integrals can only be evaluated numerically . However, Gaussian integrals can be evaluated analytically, significantly reducing computational cost. First, we define Cartesian Gaussians G_ijk :

$G_{ijk}(\textbf{r},\alpha,\textbf{I}) = x_I^i y_I^j z_I^k e^{- \alpha \mathbf{r_I}^2}$,

where the orbital angular momentum quantum number $l = i + j + k$, $\textbf{I}$ is the atom-center of interest, and $\mathbf{r_I} = \textbf{r} - \textbf{I}$.

The Cartesian Gaussians can be split into x-, y-, and z-components:

$G_{ijk}(\textbf{r},\alpha,\textbf{I}) = G_{i}(x,\alpha, I_x)G_{j}(y,\alpha, I_y)G_{k}(z,\alpha, I_z)$,

where $G_{i}(x,\alpha,I_x) = x_I^i e^{- \alpha x_I^2}$,

Next, we will require spherical-harmonic Gaussians G_lm:

$G_{lm}(\textbf{r},\alpha,\textbf{I}) = S_{lm}(x_I, y_I, z_I) e^{- \alpha \mathbf{r_I}^2}$

where l and m are the orbital angular momentum and magnetic quantum numbers, and $S_{lm}(\textbf{r}_A)$ are real solid harmonics .

Gaussian product rule

We include an important definition for subsequently evaluating integrals, the Gaussian product rule (i.e., the product of two Gaussians is also a Gaussian) .

Click to reveal the Gaussian product rule

Using this rule, the Gaussian overlap distribution Ω_ab(r) can be defined as:

$\Omega_{ab}(\textbf{r}) = G_a(\textbf{r})G_b(\textbf{r})$,

where $G_a(\mathbf{r}) = G_{ijk}(\textbf{r},a,\textbf{A})$.

The overlap distribution between two Gaussians on a line along x is itself a Gaussian:

$\Omega_{ab}^x = e^{-a x_A^2} e^{-b x_B^2} = e^{-\mu X_{AB}^2} e^{-p x_P^2} = K_{ab}^x e^{-p x_P^2}$,

where the total exponent $p = a + b$, the reduced exponent $\mu = \frac{ab}{a + b}$, the center-of-charge coordinate $P_x = \frac{aA_x + bB_x}{p}$ (recalling that $\textbf{r}_P = \textbf{r} - \textbf{P}$), the relative coordinate $X_{AB} = A_x - B_x$ (or $\mathbf{R}_{AB} = \mathbf{A} - \mathbf{B}$), and the first factor is the pre-exponential factor $K_{ab}^x = e^{-\mu X_{AB}^2}$

Overlap integral

The Gaussian product rule simplifies the evaluation of integrals. We will use the Obara-Saika scheme to present recurrence relations for the various integrals without including the derivations; those interested can refer to the referenced books and papers .

Click to reveal the overlap integral evaluation using a Gaussian basis

The overlap integrals S_ab are expressed in this scheme as:

$S_{ab} = \langle G_a | G_b \rangle = S_{ij}S_{kl}S_{mn}$,

where i,j,k and l,m,n are the orbital angular momentum quantum numbers about each Cartesian axis for G_a and G_b, respectively,

e.g., the integral of the overlap matrix about the x-axis $\Omega_{ij}^x$ is:

$S_{ij} = \int_{-\infty}^{\infty} \Omega_{ij}^x dx$.

The Obara-Saika recurrence relations for S are then defined as:

$S_{i+1,j} = X_{PA}S_{ij} +\frac{1}{2p}(iS_{i-1,j} + jS_{i,j-1})$

$S_{i,j+1} = X_{PB}S_{ij} +\frac{1}{2p}(iS_{i-1,j} + jS_{i,j-1})$

and the recurrence is begun from the overlap integral for the spherical Gaussian:

$S_{00} = \sqrt{\frac{\pi}{p}}e^{-\mu X_{ab}^2}$

Utilising the recurrence relations, the overlap integrals for arbitrary quantum numbers can be obtained. The relatively 'simple' overlap integral S_ab is then used to evaluate the remaining integrals. Equivalent recurrence relations exist for y and z that we omit here for brevity's sake.

Kinetic energy integral

The kinetic energy integral T_ab:

$\langle \phi_a | \hat{T} | \phi_b \rangle = T_{ab} = -\frac{1}{2} \langle G_a | \nabla ^2 | G_b \rangle$

can be evaluated for the one-dimensional kinetic energy integrals as:

$T_{i+1,j} = X_{PA} T_{ij} + \frac{1}{2p}(iT_{i-1,j} + jT_{i,j-1}) + \frac{b}{p}(2aS_{i+1,j} - iS_{i-1,j})$

$T_{i,j+1} = X_{PB} T_{ij} + \frac{1}{2p}(iT_{i-1,j} + jT_{i,j-1}) + \frac{a}{p}(2bS_{i,j+1} - iS_{i,j-1})$

$T_{00} = [a - 2a^2(X_{PA}^2 + \frac{1}{2p})]S_{00}$

One-electron Coulomb integral

The integrals become more complex when evaluating the Coulomb integrals.

Click to reveal the one-electron Coulomb integral evaluation using a Gaussian basis

These do not have an analytic representation but one can be found using the nth-order Boys function F_n , which is related to the error function and incomplete gamma function:

$F_n(x) = \int_0^1 e^{-xt^2}t^{2n} dt$

where $x \geq 0$.

We start with the one-electron Coulomb integrals $\Theta_{ijklmn}^N$, where i,j,k and l,m,n are the orbital angular momenta about the Cartesian axes for the basis functions a and b, respectively, and N is a non-zero integer, with N = 0 denoting the final Coulomb integrals .

The Obara-Saika recurrence relations for the one-electron Coulomb integrals are :

$\Theta_{i+1,j,k,l,m,n}^N = X_{PA} \Theta_{ijklmn}^N + \frac{1}{2p}(i\Theta_{i-1,j,k,l,m,n}^N + j\Theta_{i,j-1,k,l,m,n}^N)\\ \hspace{2cm} - X_{PC} \Theta_{ijklmn}^{N+1} - \frac{1}{2p}(i\Theta_{i-1,j,k,l,m,n}^{N+1} + j\Theta_{i,j-1,k,l,m,n}^{N+1})$

$\Theta_{i+1,j,k,l,m,n}^N = \Theta_{i,j+1,k,l,m,n}^N - X_{AB}\Theta_{ijklmn}^N$

beginning from the scaled Boys function:

$\Theta_{000000}^N = \frac{2 \pi}{p} K_{ab}^{xyz} F_N(p R_{PI}^2)$,

where K is the pre-exponential factor previously defined.

and the Coulomb integral:

$\Theta_{ijklmn}^0 = ( a | V_{ne} | b )$,

so for two 1s orbitals :

$\Theta_{000000}^0 = ( a | V_{ne} | b ) = \frac{-2 \pi}{a + b} Z_I e^{-\frac{ab}{a+b}|\mathbf{A}-\mathbf{B}|^2} F_0[(a+b)|\mathbf{P}-\mathbf{I}|^2]$.

Two-electron Coulomb integral

The two-electron integrals $\Theta_{abcd}^N$ use a slightly different notation with a,b,c,d denoting the individual Gaussian functions' angular momenta, which in turn have x-, y-, and z-angular momentum components, and N which is a non-zero integer, with N = 0 denoting the final Coulomb integrals. Evaluating these integrals is a significant challenge.

Click to reveal the integral evaluation for a Gaussian basis

The two-electron integrals are evaluated, starting from:

$\Theta_{0000}^N = \frac{2\pi^{5/2}}{pq \sqrt{p+q}} K_{ab}^{xyz} K_{cd}^{xyz} F_N(\alpha R_{PQ}^2)$

$\Theta_{ijkl}^0 = g_{ijkl} = (ij|kl)$

where i,j,k,l have the corresponding Gaussians G_a,G_b,G_c,G_d, P is the center between A and B, Q is the center betwen C and D, and $\alpha = \frac{pq}{p+q}$ is the reduced exponent.

So, for four 1s orbitals it would be :

$\Theta_{0000}^0 = g_{0000} = (00|00) = \frac{2\pi^{5/2}}{(a+b)(c+d)(a+b+c+d)^{1/2}} e^{-\frac{ab}{a+b}|\mathbf{A}-\mathbf{B}|^2 - \frac{cd}{c+d}|\mathbf{C} - \mathbf{D}|^2} F_0[\frac{(a+b)(c+d)}{(a+b+c+d)}|\mathbf{P}-\mathbf{Q}|^2]$.

A set of two-electron integrals can then be generated using a four-term version of the Obara-Saika recurrence relations :

$\Theta_{i+1,0,0,0}^N = X_{PA}\Theta_{i000}^N - \frac{\alpha}{p}X_{PQ}\Theta_{i000}^{N+1} + \frac{i}{2p}(\Theta_{i-1,0,0,0}^N - \frac{\alpha}{p} \Theta_{i-1,0,0,0}^{N+1})$

$\Theta_{i,0,k+1,0}^N = -\frac{bX_{AB} +dX_{CD}}{q} \Theta_{i0k0}^N + \frac{i}{2q} \Theta_{i-1,0,k,0}^N + \frac{k}{2q} \Theta_{i,0,k-1,0}^N - \frac{p}{2q} \Theta_{i+1,0,k,0}^N$

$\Theta_{i,j+1,k,l}^N = \Theta_{i+1,j,k,l}^N + X_{AB} \Theta_{ijkl}^N$

$\Theta_{i,j,k,l+1}^N = \Theta_{i,j,k+1,l}^N + X_{CD} \Theta_{ijkl}^N$

This completes the integral evaluation using GTOs required for calculating the total energy. The following section will evaluate the integrals when using a plane-wave basis.

Planewaves

The Gaussian orbital integral evaluation requires many equations, even though we have omitted the derivations. The plane-wave integral evaluations can be expressed in simpler equations. Since plane waves are non-local, the angular momentum does not need to be explicitly included.

Mind: the equations below are for the potentials - the standard way for plane waves. Each of these integrals needs to be multiplied by the density $n(\mathbf{G})$ to obtain the energy.

Starting with the kinetic energy integral in real space $\langle \hat{T} \rangle$ for a specific k-point $\mathbf{k}$ :

$\langle \mathbf{k}+\mathbf{G'} | \hat{T} | \mathbf{k}+\mathbf{G} \rangle = -\frac{\hbar^2}{2m} \int d^3r e^{-i(\mathbf{k}+\mathbf{G'}) \cdot \mathbf{r}} \nabla^2 e^{-i(\mathbf{k} + \mathbf{G}) \cdot \mathbf{r}}$

In reciprocal space, it is easier to express. By taking a Fourier transform, the integral becomes:

$\langle \mathbf{k}+\mathbf{G'} | \hat{T} | \mathbf{k}+\mathbf{G} \rangle = \frac{\hbar^2 |\mathbf{k}+\mathbf{G}|^2}{2m} \delta_{\mathbf{G}, \mathbf{G'}}$

Skipping over similar derivations for the remaining integrals, the ionic potential integral $\langle \hat{V}_{ion} \rangle$ can be expressed as:

$\langle \mathbf{k}+\mathbf{G'} | \hat{V}_{\text{ion}} | \mathbf{k}+\textbf{G} \rangle = -4 \pi \varepsilon_0 e^2 \frac{ Z }{|\mathbf{G - G'}|^2} S^{\kappa}, (\mathbf{G - G'}) \neq 0$,

where $S^{\kappa}$ is the structure factor summed over each species (nucleus) $\kappa$ at position $\tau_{\kappa, j}$ from j to $n^{\kappa}$:

$S^{\kappa}(\mathbf{G}) = \sum_{j=1}^{n^{\kappa}} e^{i\mathbf{G} \cdot \tau_{\kappa, j}}$.

Finally, we consider the Coulomb, or Hartree, integral $\langle \hat{V}_{H} \rangle$:

$\langle \mathbf{k}+\mathbf{G'} | \hat{V}_{\text{H}} | \mathbf{k}+\textbf{G} \rangle = 4 \pi \varepsilon_0 e^2\frac{n(\mathbf{G - G'})}{|\mathbf{G - G'}|^2}, (\mathbf{G - G'}) \neq 0$.

where $n(\mathbf{G - G'})$ is the density:

$n_{i,\mathbf{k}}(\mathbf{G}) = \frac{1}{\Omega} \sum_m c_{m,i}^*(\mathbf{k}) c_{m'',i}(\mathbf{k})$,

where $m''$ denotes the $\mathbf{G}$ vector for which $\mathbf{G}_{m''} \equiv \mathbf{G}_{m} + \mathbf{G}$.

The evaluation of the Coulomb interaction using plane waves can be treated "locally" in reciprocal space as the product of the total density, i.e., the each electron interacts collectively with all the other electrons, scaling at $O(Nlog(N))$, where N is the number of grid points . This is significantly cheaper than evaluating using GTOs, where the two-center electron repulsion integrals (ERIs) must be evaluated directly, scaling at nominally $O(N^4)$, where N is the number of basis functions, though approximations can be made to reduce this to $O(N^2)$ . GGAs using plane waves are therefore significantly cheaper than using GTOs.

The exchange-correlation integral $\langle \hat{V}_{xc} \rangle$ is evaluated in real space and then Fourier transformed to reciprocal space. Since it depends on the individual density functional used, we do not show it here. For hybrid functionals, the exchange $\langle \hat{V}_{x} \rangle$ must also be considered:

$\langle \mathbf{k}+\mathbf{G}' | \hat{V}_x | \mathbf{k}+\mathbf{G}\rangle = -\frac{4\pi e^2}{\Omega} \sum_{\mathbf{G}''} \frac{c_{\mathbf{G}'-\mathbf{G}'',i}^*(\mathbf{k}) c_{\mathbf{G}-\mathbf{G}'',i}(\mathbf{k})} {|\mathbf{G}''|^2}$

A key point of difference between GTOs and plane waves appears when evaluating the exchange interaction, which is non-local, i.e., each electron interacts with every other electron, necessitating all pair-wise interactions to be considered. As a result, it must be expressed in terms of the orbitals, rather than the density. It is a convolution in reciprocal space, rather than a product. This scales at $O(N^2)$ with respect to grid points. In GTOs, evaluating the exchange integral scales at $O(N^4)$, which can be reduced to $O(N^3)$ with respect to basis functions . Since GTOs are a local basis, the integrals can be screened such that not all exchange integrals need to be evaluated. As a result, hybrid calculations using GTOs are not significantly more costly than for GGAs, ~1.5 times the cost . Plane waves cannot screen integrals in this way, so hybrid calculations using plane waves are much more expensive than GGA.

Having expressed all the integrals for both GTOs and plane waves, it is reasonable to conclude that the integral evaluation is, in general, simpler in a plane-wave basis than Gaussian. This difference becomes clear when selecting the basis for a calculation.

Selecting the basis

Calculations using a GTO basis face several important challenges: first, the basis must be selected, second, convergence to the complete basis is often challenging, and third, basis set superposition errors must be avoided.

For selecting the basis, there are a plethora of bases to choose from , e.g., Ahlrichs' split-valence (def2-XZVP(PD)) , Dunning's correlation-consistent ((aug-)cc-pVXZ) , among others shown in the basis set exchange . X denotes how many basis functions are used to describe a particular atomic orbital, according to the exponential coefficient 'zeta' ζ. Choosing the correct basis can be particularly difficult. To reach converged results, it is often necessary to use triple-zeta bases and extrapolate to the complete basis set (CBS) limit . For heavier elements, it is common to use effective core potentials (ECPs), pseudopotentials that model the interactions of core electrons using a potential instead of explicitly, resulting in significantly reduced computational cost . These will be discussed in more detail below.

Besides the difficulty of choosing a basis, even when a basis has been chosen, the incompleteness of the basis can introduce further erroneous interaction energies, the basis-set superposition error (BSSE) , as one molecule uses the orbitals on a neighboring molecule to reduce its own energy, effectively increasing its basis. The BSSE must be corrected, e.g., using the counterpoise correction (CPC) scheme .

Plane waves in a 2D 11x11 grid in reciprocal space, with labeled grid intergers m₁ and m₂. The blue dot in the center is a k-point, in this case the Γ-point, lying within the first Brillouin zone (BZ), the black box in the center. Plane waves are show as vectors (red arrows) according to their momentum G in terms of the unit reciprocal lattice vectors (b₁ and b₂), directed to a neighboring grid point. Note that these momenta are exactly the same as the momenta shown in the plane-wave introductory section. The concentric (red) circles intersecting grid points are the radii of energetically equivalent plane waves (i.e., those with identical momenta). As the length of the plane-wave vector increases, the radii increase up to the energy cutoff G_cut (blue circle). These plane waves constitute the basis for a calculation.

Plane waves address some of the problems of a GTO basis:

• Selecting the basis

Each plane wave has an associated kinetic energy E_PW and a momentum G:

$E_{PW} = \frac{\hbar^2}{2m} G^2$.

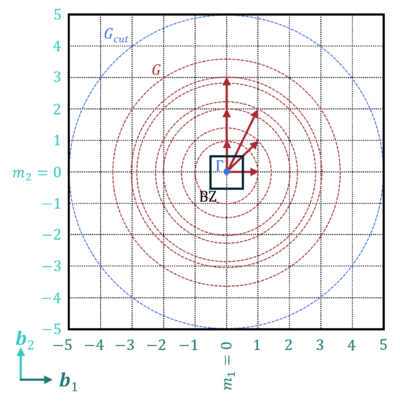
A reciprocal lattice vector G is defined as:

$\mathbf{G} = m_1 \mathbf{b}_1 + m_2 \mathbf{b}_2 + m_3 \mathbf{b}_3$,

and m are integers and b are the unit reciprocal lattice vectors.

The $m_i \cdot b_i$ are regular points in reciprocal space, i.e., they define the fast Fourier transform (FFT) grid used in plane-wave codes.

• Convergence of the basis

The maximum value of m_i is the number of grid points, defined by the plane-wave kinetic energy cutoff E_cut:

$E_{cut} = \frac{\hbar^2}{2m} G_{cut}^2$,

where G_cut is the plane-wave momentum cutoff and sets the maximum value for the grid points, and m₁ = NGX, m₂ = NGY, and m₃ = NGZ.

A single number energy cutoff defines the plane-wave basis:

$|\mathbf{G} + \mathbf{k}| < G_{cut}$,

including plane waves of up to that momentum (or energy) (see figure).

The number of plane waves N_PW (the number of plane waves in VASP can be found using by searching for NPLWV in the OUTCAR file) is related to the energy cutoff E_cutoff and the size of the cell Ω₀:

$N_{PW} \propto\ \Omega_0\ E_{cutoff}^{3/2}$

The difficulty of selecting a specially polarized, diffuse, or augmented basis necessary when using GTOs is already accounted for by the plane-wave basis, by virtue of it being non-localized.

• Basis set superposition error

Since the basis is not localized, the BSSE does not occur. Additionally, as the basis set is defined by a single number, the CBS limit can be approached systematically. Describing the core electrons using plane waves is costly. Instead, pseudopotential are commonly used. The generation of these pseudopotentials introduces is complex. However, many are already available in to select, which reduce the number of plane waves required signficantly.

Pseudopotentials

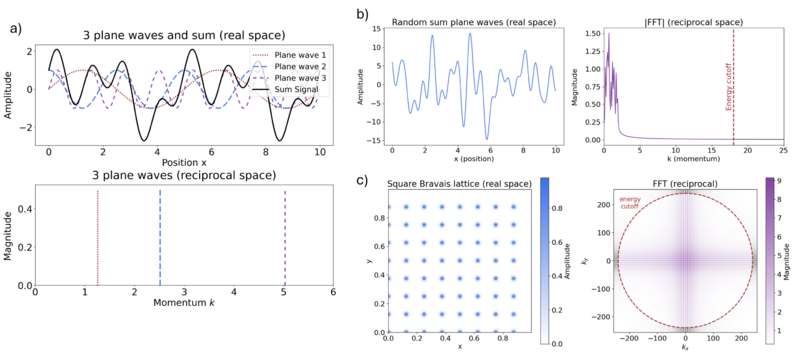
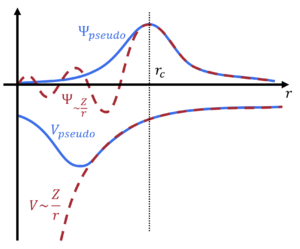
It is simple to define the basis using plane waves. However, describing the nodal oscillations in the wavefunction close to the nucleus would require many plane waves, reaching cutoffs of 100-1000 keV (hundreds of thousands to millions of plane waves) for all-electron (AE) calculations even when using a smooth potential . This can be seen in our earlier plane-wave figure, where it is clear that much larger plane-wave momenta are required to model the "nuclei" in the Bravais lattice, ~200 (Figure c), compared to ~20 for the periodic function. To solve this, a pseudopotential is used to describe close to the nucleus exactly within a core radius r_c, reducing the number of plane waves required. Several types of pseudopotentials are available, e.g., ultrasoft pseudopotentials (USPPs) and the projector augmented-wave (PAW) approach . Specifically, the PAW approach is used in VASP. In this way, the CBS limit can be more easily reached. The PAW approach is comparable to pseudopotentials, effective core potential (ECP), commonly used for heavy elements in GTO codes.

Effective core potentials

The ECP Hamiltonian H_ECP can be expressed as :

$H_{\text{ECP}} = -\frac{\hbar^2}{2m} \nabla^2 + V_{H}(\mathbf{r}) + V_{\text{xc}}(\mathbf{r}) + V_{\text{ECP}}(\mathbf{r})$

where the ECP potential $V_{\text{ECP}}(\mathbf{r})$ is defined as:

$V_{\text{ECP}}(\mathbf{r}) = V_{\text{local}}(r) + \sum_l V_{l}(r) P_l$

where V_local is the electron-core interactions and is a screened form of the electron-nucleus interaction (cf. V_ne and V_ion), V_l are the radial components of the potential, and the projector operator P_l onto states of angular momentum l is given by:

$P_l = \sum_m | \chi_{lm} \rangle \langle \chi_{lm} |$

where χ are atom-like functions.

Projector augmented-wave approach

Sketch of a pseudopotential V_pseudo and pseudowavefunction ψ_pseudo in the PAW. The wavefunction ψ and the potential V are described exactly within the core radius r_c (red). Outside, the core wavefunction and the potential are described by the pseudowavefunction and pseudopotential (blue). Plane waves then describe the interaction of the valence bands.

In VASP, the projector-augmented wave (PAW) approach is used . In the PAW approach, the one-electron wavefunctions $\psi_{n\mathbf{k}}$, the orbitals, are derived from pseudo-orbitals $\widetilde{\psi}_{n\mathbf{k}}$ by means of a linear transformation:

$|\psi_{n\mathbf{k}} \rangle = |\widetilde{\psi}_{n\mathbf{k}} \rangle + \sum_{i}(|\phi_{i} \rangle - |\widetilde{\phi}_{i} \rangle) \langle \widetilde{p}_{i} |\widetilde{\psi}_{n\mathbf{k}} \rangle.$

The pseudo-orbitals $\widetilde{\psi}_{n\mathbf{k}}$ (where $nk$ is the band index and k-point index) describes the smooth wavefunction beyond the cutoff radius r_c, i.e., the interstitial region (outside of the augmentation (PAW) spheres ), where they match the AE orbitals $\psi_{n\mathbf{k}}$. The $\widetilde{\psi}_{n\mathbf{k}}$ are described by plane waves.

Inside r_c, the pseudo- and AE orbitals do not match. This difference is corrected by mapping $\widetilde{\psi}_{n\mathbf{k}}$ onto $\psi_{n\mathbf{k}}$ using pseudo partial waves $\widetilde{\phi}_{\alpha}$ and AE partial waves $\phi_{\alpha}$ ($\alpha$ refers to the atomic site, angular momentum quantum numbers and references energies). The partial waves are local to each ion, i.e., onsite, and so are calculated on a radial grid. They are described by each PAW pseudopotential and derived from the solutions of the radial Schrödinger equation for a non-spinpolarized for a reference atom. The pseudo- and AE partial waves are related to one another by projector functions $\widetilde{p}_i$, which are dual to the partial waves.

The PAW method expresses the all-electron (AE) wavefunction (red). The pseudo-wavefunction (blue) is described in plane waves, with the difference between the AE and pseudo-wavefunction made within the core radius (black circles) about the nuclei (black dots) on the radial grid.

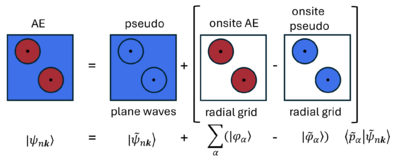
The PAW method implemented in VASP exploits the commonly-used frozen core (FC) approximation. The core electrons are kept frozen in the configuration for which the PAW dataset was generated. In the PAW approach, the interaction of core electrons with the valence electrons are included, via the core electron's density and pseudo-density. When required, the core states can be reconstructed, e.g., for NMR calculations.

The PAW Hamiltonian H_PAW can be expressed as :

$H_{\text{PAW}} = -\frac{\hbar^2}{2m} \nabla^2 + \tilde{V}_{\text{ion}}(\mathbf{r}) + \tilde{V}_H(\mathbf{r}) + \tilde{V}_{\text{xc}}(\mathbf{r}) + \sum_{ij} | \tilde{p}_i \rangle D_{ij} \langle \tilde{p}_j |$

where Ṽ are the operators for the PAW method (specifically the pseudo-wavefunction), D_ij accounts for the difference between the all-electron (AE) wavefunction and pseudowavefunction ($D_{ij} = \hat{D}_{ij} + D_{ij}^1 - \tilde{D}_{ij}^1$ which are the compensation charge (ensures the the correct density within the augmentation sphere), onsite, and pseudo-onsite terms for D, respectively), and $| p_i \rangle \langle p_j |$ are the projector functions, analogous to $P_l$ for the ECP, and relate the pseudowavefunction to the AE wavefunction within the core radius r_c.

Comparing ECP and PAW

The choice of basis set is difficult when using GTOs, with many different GTO bases available, all generated according to different preferences. The same is true of ECPs, though these are more easily defined for using GTOs, by only a few coefficients and exponents . The respective equations for the Hamiltonians are analogous, with the selection of projectors being one of the key differences. For a plane-wave basis, the choice of basis is simple, it is the generation of the pseudopotential that is difficult, which requires specialist care. VASP uses its own set of optimized PAW pseudopotentials: the POTCAR files. The standard POTCAR when used with the default energy cutoff (cf. ENMAX in POTCAR) are close to the CBS limit, though this needs to be tested in each case. For more difficult problems, harder POTCARs with smaller core radii are available.

The treatment of core electrons is a another key difference between the ECP and PAW approaches, besides using GTO and plane-wave bases. In an ECP, the core electrons are completely removed and replaced by a potential, only the wavefunctions of the valence electrons are treated.

Mind: There is no standardized repository of pseudopotentials that all plane-wave codes use. Therefore the absolute energies do not agree between different codes and depend on the pseudopotential. Only energy differences (e.g., adsorption energies, atomization energies) are comparable between different plane-wave codes.

Methods

When using a GTO basis, it is typical to use density functional theory (DFT) to solve many molecular problems. The Hartree-Fock (HF) is typically only used to generate orbitals for use with post-HF methods such as Møller-Plesset perturbation theory (e.g., MP2), the coupled cluster (CC) approach, etc.

In a plane-wave basis, HF is rarely used, with DFT being predominant. Typically, the local density approximation (LDA), generalized gradient approximation (GGA), meta-GGAs (mGGA), and hybrid functionals are used, as well as non-local van der Waals functional. Occasionally, post-HF calculations are done, though these are based on DFT, rather than HF.

Post-Hartree-Fock

One reason for the limited use of post-HF calculations in plane-wave codes, and solid-state more generally, is the large prefactor required to perform a calculation, resulting in an initial high cost. When using GTOs by comparison, the prefactor is small, so small- to medium-sized molecules are readily calculable. However, the scaling of methods in GTO codes is a significant limiting factor, e.g., for system size N, O(N⁵) for MP2, O(N⁶) for CCSD, and O(N⁷) for CCSD(T), making large molecules infeasible. For plane-wave codes, the initial cost is high due the number of k-points required. However, the scaling is much lower, with FFT of orbitals between real and reciprocal space scaling at O(N²log(N)) for DFT, O(N⁴) for the random-phase approximation (RPA) (a sort of CCSD) compared to O(N⁶) in GTOs, and O(N³) or O(N⁴) for quantum Monte Carlo (QMC) .

Important: Note that lower scaling implementations of RPA, e.g., O(N3) in plane wave, and O(N4log(N)) in GTO exist ).

Using GTOs, a cluster can be used to model a surface or solid. With increasing cluster size, this will gradually approach the periodic limit. For small to medium clusters, GTOs will be more cost-effective due to the small prefactor. However, as increasingly large clusters are used, there comes a cross-over point where the high scaling of GTO methods is greater than the large prefactor for plane waves, so the lower scaling of plane waves gives them the edge. The downside is that there are many virtual orbitals (conduction states) when using plane waves and it is necessary to include many of these.

Mind: The plane waves are inherently delocalized. Bands can be localized to molecular orbitals using Wannier functions. However, applying post-HF methods using Wannier functions is not routinely done. There are specialist techniques where the conduction bands are projected onto atomic orbitals to create a smaller basis for performing coupled cluster calculations .

Several post-HF methods are available, for example, the familiar MP2. An alternative method is the RPA, which can be used to calculate the correlation energy. The RPA can be considered from a few different directions, the most familiar of which to those coming from a GTO basis, is coupled cluster. The RPA is coupled cluster doubles (CCD) with only the ring diagrams included (rCCD) ; additionally, in the exchange diagrams are typically excluded, making it direct ring CCD (drCCD) . The bands do not need to be converted to localized orbitals, as the correlation energy is calculated via the response function in the adiabatic-correction-fluctuation-dissipation theorem (ACFDT) . Using finite-order perturbation theory (e.g., MP2), the correlation energy diverges for metals, due to their zero-band gap. RPA is an exception to this, allowing the application of post-HF methods to metals.

Additionally, there has been some use of coupled cluster (e.g., CCSD(T)) in solid-state physics . This is an area of active research . An alternative method that can more accurately describe the system is quantum Monte Carlo (QMC) . This is not typically done within the PAW approach, though implementations do exist . Both coupled cluster and QMC are computationally costly and are still developing areas.

Excited states

A final difference is in how excitations are treated. While multi-reference calculations are commonly used in GTO codes , multi-reference is never used in PW codes, QMC excepted, with only a single Slater determinant being used, which is sufficient for most solid-state systems. Modeling optical properties is commonly utilising time-dependent density functional theory (TDDFT), RPA, the GW approximation, and the Bethe-Saltpeter equation (BSE).

Going from local to periodic calculations

Besides the theoretical differences, there are also a few practical differences when using a periodic code, instead of a local one.

k-points

Plane waves in a 2D 11x11 grid in reciprocal space with a second k-point k' (purple dot) added, showing the plane waves (green arrows) from k'. Plane waves expanding from k' are show in green circles of momentum G, up to the energy cutoff G_cut (purple circle). Inside the BZ, an equivalent point to k' is shown as a hollow, purple circle. The previous plane-wave expansion image is shown in greyscale.

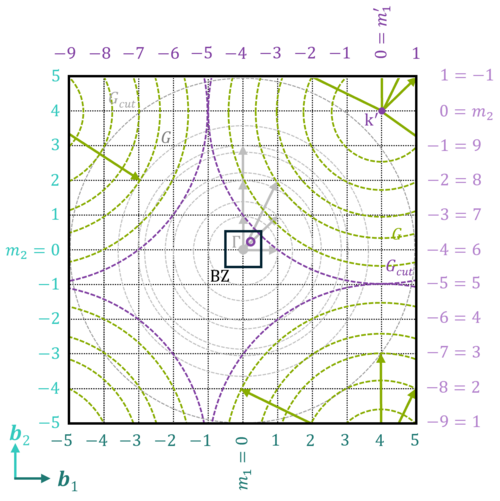
For example, the k-point mesh that is used is very important. The first Brillouin zone (BZ) is the uniquely defined primitive cell in reciprocal space and, according to Bloch's theorem, integration over the BZ is sufficient to describe the entire wavefunction. However, analytic integration over the BZ is not feasible, so instead a selection of well-placed points inside the BZ is chosen until the integral is converged. These points are in reciprocal (or momentum, k) space, also known as k-space, so these points are referred to as k-points. A k-point mesh is defined, e.g., using a KPOINTS file, and must be incrementally increased to obtain converged results. The k-point mesh must be tested, equivalent to ensuring that a sufficiently large basis is used (e.g., increasing the plane-wave energy cutoff or going from a double zeta to triple zeta GTO basis).

For plane waves, the number of plane waves used is increased to achieve convergence within the unit cell, equivalent to using a larger GTO basis, approaching the CBS. With more k-points in reciprocal space, the effective size of supercell used in real space is increased. By using more k-points, you effectively use a larger supercell, improving the description, analogous to using a larger cluster to model a surface.

Smearing

The smearing of the orbital occupation is also important. With GTOs, you tend to look at molecules, and with plane waves, solids. Typically the HOMO-LUMO gap (band gap in solids) is smaller in solids than in molecules (insulators are an important exception in solids; degenerate or closely-lying states requiring multi-reference calculations for molecules). When the gap is small, e.g., in metals and semi-conductors, smearing becomes important to aid convergence. Smearing is used to create a gradual distribution of electron occupation between valence (occupied) and conduction (unoccupied) bands, avoiding unphysical oscillations in the density that are created when the population varies in a step-like way. There are several different smearing options available in VASP.

Vacuum

A third point is in the treatment of the vacuum. In a GTO basis, the system is isolated and surrounded by a vacuum without additional cost. In a plane-wave basis, it is the periodic cell that is described, so any vacuum (e.g., surrounding an isolated molecule, above a surface) increases the cost of the calculation. The vacuum is, therefore, something that should be tested for your system. Minimizing the vacuum while achieving convergence is important to test to reduce the cell size and thereby the cost of calculation. The vacuum can also be reduced by truncating the Coulomb kernel to remove electrostatic interactions with periodic replicas in non-periodic directions.

Pulay stress

A final factor to be considered in periodic calculations is the Pulay stress . This is the plane-wave analogue of the basis-set superposition error (BSSE). With BSSE, one molecule can reduce its own energy using a neighboring molecule's basis; it is an issue of an incomplete Gaussian basis, resulting in overestimating binding energies and, therefore, decreasing the distance between molecules. With Pulay stress, the plane-wave basis is incomplete (recall that it is related to the cell volume), and so, when the cell changes size, i.e., during a structure relaxation, the basis changes. This results in an improved basis for smaller cells, and hence, a non-physical stress is felt by the periodic cell, Pulay stress. The Pulay stress erroneously decreases the equilibrium unit cell parameter and creates improper volume-energy curves. In each case, using a more complete basis is the solution to this. BSSE uses the CPC scheme and a larger zeta-basis, while Pulay stress can be solved by using a higher energy cutoff and a denser k-point mesh.

Comparing Gaussian and plane-wave approaches

A large distinction is seen between Gaussian and plane waves when it comes to the types of methods used. Plane-wave codes most often use DFT, while post-HF methods are less frequently used. GTOs can be readily applied to perturbation methods, coupled cluster, and other post-HF methods, including multireference methods. Regardless of basis, post-HF methods are expensive are limited to relatively small systems. Small- to mid-sized molecules can be readily studied using post-HF methods using a Gaussian basis, while larger ones become quickly infeasible. In contrast, even small systems are a challenge for post-HF using plane waves, but if they are computationally feasible, then larger ones are likely accessible.

Moving on to the basis, many basis sets are available for GTOs. However, reaching the basis set limit is difficult, resulting in basis set incompleteness errors (BSIE) and basis set superposition errors (BSSE). The basis set is more easily selected using plane waves, defined by a single number, the energy cutoff. Plane waves struggle to describe the rapid oscillations of the orbitals close to the nucleus. Using PAW potentials can solve this, allowing the basis set limit to be systematically reached by changing the energy cutoff. Selecting the basis using a plane-wave basis is easy, in contrast to the difficulty of generating suitable pseudopotentials. In VASP, good PAW pseudopotentials have already been generated, so this does not generally need to be considered. The evaluation of integrals is far easier using plane waves than it is with GTOs, where it can create significant issues.

Plane waves and GTOs are complementary approaches to modeling electronic structure. GTOs are often better for calculating small- to medium-sized molecules, while plane waves are better suited to periodic systems and molecules (with a large vacuum). For intermediate systems, e.g., molecules on surfaces, both methods can be used, with cluster models for GTOs and the periodic slab approach for plane waves. In recent years, the cluster model has been largely superseded by the periodic slab approach. Whether plane waves or GTOs are better depends on the individual problem being investigated, with each approach bringing its own challenges. VASP can be used to model periodic systems such as bulk systems [1] and surfaces [2], and molecules [3] using a variety of methods, which are introduced in our tutorials [4].