Category:2D materials

From VASP Wiki

Every real crystal or material has a surface. In VASP simulations, however, periodic boundary conditions typically model an infinite crystal, the perfect bulk. To model a surface, a thin film, or an intrinsically 2D material, therefore, requires breaking these periodic boundary conditions intentionally. This is done by elongating the simulation cell in one direction (normal to the intended surface) without adding more atoms. This creates a vacuum region between repeated images of thin films of material (commonly called surface slabs, or just slabs), each of which has two surfaces.

Mind: It is not possible to create only a single surface in an atomistic model with periodic boundary conditions. Cleaving a bulk material inevitably produces two surfaces. These two surfaces are generally nonequivalent, although they may be identical depending on the material and the cleavage plane.

Nomenclature

Surfaces

As discussed above, in atomistic simulations employing periodic boundary conditions, surfaces are modeled as thin films of a material separated by a vacuum region of sufficient thickness. When the surface itself is the primary focus, the slab model must be constructed to mimic a semi-infinite bulk crystal beneath the surface. The second surface, located on the opposite side of the slab, should be sufficiently separated to prevent strong interactions between the two surfaces.

Thin films

Although thin-film simulations often employ the same computational setup and slab model as surface calculations, their objective differs. In thin-film studies, the goal is to investigate the behavior and properties of the entire system — including both surfaces and the bulk-like interior region — rather than isolating the characteristics of a single surface.

2D materials

This class of materials comprises ultrathin films consisting of only a few atomic layers. Prototypical examples include graphene, which is one atomic layer thick, and molybdenum disulfide (MoS$_2$), which consists of three atomic layers. Such materials can occur naturally as van der Waals–bonded layered crystals, but they can also be exfoliated and studied as mono-, bi-, or few-layer systems.

Slab symmetry and stoichiometry

Fig 1. Side (a) and top (b) view of a symmetric and stoichiometric, 6-layer-thick NaCl 001 slab.
Fig 2. Side (a) and top (b) view of a non-symmetric but stoichiometric, 6-layer-thick NaCl 111 slab.
Fig 3. Side (a) and top (b) view of a symmetric but non-stoichiometric, 5-layer-thick NaCl 111 slab.

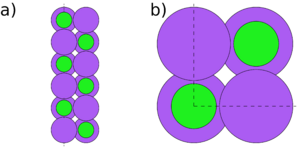
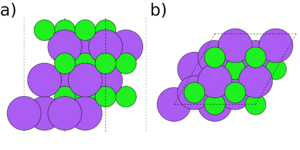
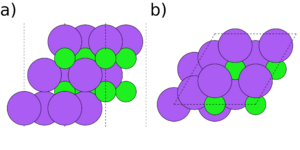
Symmetry and stoichiometry are important concepts for surface slabs. Figs. 1 to 3 show three different surface slabs of NaCl, a 001 and two 111 slabs. All 001 lattice planes contain an equal amount of Na and Cl atoms, so slabs of all thicknesses are both symmetric (both surfaces are equivalent) and stoichiometric (the bulk ratio 1:1 of the atom types is preserved in the slab). The 111 lattice planes contain either Na or Cl. Thus, the slabs can either be stoichiometric (Fig. 2) or symmetric (Fig. 3), but it is impossible to achieve both.

Slab symmetry

If a slab is non-symmetric, it is important to consider dipole corrections. The non-symmetric 111 NaCl slab (Fig. 2) is forming a dipole, with $Cl^{-}$ and $Na^{+}$ terminations on opposite sides of the slab. This leads to a potential gradient through the vacuum, which is not physical and leads to extra interaction between the slab replicas. In general, this can be true for any non-symmetric slabs, not only for ionic crystals like NaCl. In those cases, dipole corrections should always be turned on and the size of the dipole checked in the OUTCAR file. However, energy differences due to dipole interactions are usually smaller than energy differences due to a different exchange-correlation functional. They can also interfere with convergence during relaxations. It is thus usually advisable to initially relax the system without dipole corrections and then turn on the corrections in a static follow-up calculation. If there is a resulting dipole, a follow-up relaxation can be performed using the WAVECAR file from the static calculation as a starting point.

Slab symmetry is also important for surface calculations. If the two surfaces of a slab are not equal, the computation of the surface energy becomes more cumbersome.

Slab stoichiometry

Slab stoichiometry is usually less important than symmetry for the computation setup. But in surface-energy-calculation methods that reference the bulk energy (which is always stoichiometric), complications can arise.

Advice and recommendations

Creating slab models

A clean surface is defined uniquely by the bulk crystal, the lattice plane along which the cut should be placed, and the termination of the surface. For a slab model, additional parameters are important — mainly the slab thickness and the thickness of the vacuum region. Both need to be converged independently to ensure accurate results.

While it is entirely possible to create a slab model by visualizing a crystal and thinking hard about lattice planes and stacking, it is usually more convenient and less error-prone to use available tools. The Python packages ASE[1] and Pymatgen[2] both provide surface-building capabilities. The following ASE code snippet creates an NaCl (001) slab with six layers and 10 Å vacuum, for example: 

from ase.build import bulk, surface
from ase.io import write
nacl_bulk = bulk('NaCl', 'rocksalt', a=5.64, cubic=True)
slab_001 = surface(nacl_bulk, (0,0,1), 3)
slab_001.center(vacuum=10.0, axis=2)
write('POSCAR_NaCl_001_6layers.vasp', slab_001, format='vasp', direct=True, sort=True)

In-plane lattice parameters

When two surfaces are created by cleaving a crystal, bonds are broken, and energy needs to be spent. This energy is called the surface energy, and it can differ significantly between different lattice planes and surface terminations. In real materials, the surface energy is vanishingly small compared to the bonding energy in the bulk crystal, but for a surface-slab model, it can be comparatively large. Thus, the in-plane lattice parameter will usually shrink compared to the bulk crystal and depend on the number of layers in the slab.

Tip: For surface calculations, it is prudent to use the in-plane lattice parameter of the bulk, and not relax it, since the surface of a semi-infinite bulk would retain the bulk lattice parameter as well. For a thin-film calculation, however, the in-plane lattice parameters should be relaxed to relieve in-plane strain.

Out-of-plane lattice parameters

Since bonds will be cut when a surface is created, the spacing between the first two layers of the surface will usually be reduced with respect to the bulk lattice spacing. This effect is often important for the surface properties and should not be disregarded. Avoiding this relaxation on the slab side opposite to the surface of interest, however, can reduce the total number of layers needed to mimic the semi-infinite bulk.

Tip: For a surface calculation, it is often beneficial to fix several layers at the bottom of the slab to simulate the semi-infinite bulk more efficiently and with fewer total layers. The Selective Dynamics options in the POSCAR file can be used for this purpose. A thin film should be fully relaxed.

Surface-energy calculations

The surface energy, $\gamma$, is an important characteristic of any surface, determining its stability and influencing its adhesion properties, catalytic activity, and ability to form thin films and interfaces.

For a symmetric and stoichiometric surface slab, the surface energy $\gamma$ of the two equivalent surfaces is given by: \begin{equation} \gamma = \frac{1}{2A}\left[E_\mathrm{slab} - N E_\mathrm{bulk}\right] \quad, \end{equation} where $E_\mathrm{slab}$ is the total energy of the slab, $E_\mathrm{bulk}$ is the total energy of the bulk, and $N$ is the number of formula units in the slab relative to those in the bulk cell.

A more general formula, that holds for non-stoichiometric and non-symmetric slabs for the surface energies $\gamma_1$ and $\gamma_2$ on both sides of the slab is \begin{equation} \gamma_1 = \frac{1}{A}\left[E_\mathrm{slab} - \sum_i N_i\mu_i(p, T)\right] - \gamma_2 \quad, \label{eqn:gen_surfen} \end{equation} where the bulk energy is replaced by a term with the chemical potentials $\mu_i$, which influence the surface energies. Thus, the value of the temperature- and pressure-dependent chemical potential can determine which surface is energetically most favorable.

Tip: The surface energy must be converged with respect to both the number of layers and the vacuum thickness. This can be challenging. To achieve good convergence of the surface energy with respect to slab thickness, it is beneficial to use a bulk cell with the same symmetry as the surface cell to ensure equivalent k-point sampling. Another approach is to infer the bulk energy from the energies of progressively thicker slabs using the Boettger method[3].

Please also consult our tutorial on Ni(111) for more in-depth information about surface-energy calculations.

Adsorption at a surface

When studying the adsorbtion of a molecule on a surface, a lot of physical and computational options need to be considered:

  • Coverage - How many molecules are present per unit cell.
  • Adsorption site(s) – A surface can have several distinct high-symmetry positions (e.g., on-top, bridge, hollow) where a molecule can adsorb. Most of these correspond to local minima, and it is necessary to explore several possibilities to find the most stable configuration.
  • Molecular orientation – Relaxations can help determine the optimal geometry, but molecules may become trapped in local minima.
  • Van der Waals interactions – Adsorption energies are usually accurate only if a dispersion correction or a nonlocal van der Waals functional is used.
  • Dipole corrections – Adsorption of a molecule breaks the symmetry of the system and usually results in the formation of a dipole moment. Dipole corrections should be enabled, at least after relaxation of the system.

Please also consult our tutorial on CO adsorption on Ni(111) for more detailed guidance.

Computing the work function

The work function is defined as the work needed to move an electron from a surface to a point in vacuum sufficiently far away from this surface. Please consult our how-to page on computing the work function.

Simulation of STM pictures

Scanning-tunneling-microscopy (STM) pictures can be simulated by using a post-processing method to compute partial charge densities. Please consult our how-to page on partial charge densities and STM simulations.

Electrostatic corrections

As mentioned, e.g., in the slab symmetry or adsorption at a surface sections, electrostatic corrections can be important for 2D materials, thin films, and surfaces. Please consult the electrostatics and the electrostatic corrections pages for more information.

Tutorials

References

  1. ↑ https://wiki.fysik.dtu.dk/ase/ (2025).
  2. ↑ https://pymatgen.org/ (2022).
  3. ↑ J. C. Boettger, Phys. Rev. B 49, 16798 (1994).

Pages in category "2D materials"

This category contains only the following page.

E

Retrieved from "https://vasp.at/wiki/index.php?title=Category:2D_materials&oldid=32777"