Hybrid functionals: formalism: Difference between revisions
No edit summary |
No edit summary |
||
| (21 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
The hybrid functionals can be categorized into | The exchange energy in hybrid functionals is a mixture of semilocal (SL) and nonlocal Hartree-Fock (HF) types. They can be categorized into different families according to the type of semilocal approximation (LDA, GGA, or MGGA) or the treatment of the short- and long-range parts of the exchange. A rather general formula that encompasses the different families of hybrid functionals is given by | ||
:<math>E_{\mathrm{xc}}^{\mathrm{hybrid}}=a_{\mathrm{SR}} E_{\mathrm{x,SR}}^{\mathrm{HF}}(\mu) + a_{\mathrm{LR}} E_{\mathrm{x,LR}}^{\mathrm{HF}}(\mu) + (1-a_{\mathrm{SR}})E_{\mathrm{x,SR}}^{\mathrm{SL}}(\mu) + (1-a_{\mathrm{LR}})E_{\mathrm{x,LR}}^{\mathrm{SL}}(\mu) + E_{\mathrm{c}}^{\mathrm{SL}}</math> | |||
where | |||
*<math>a_{\mathrm{SR}}</math> and <math>a_{\mathrm{LR}}</math> are the '''mixing parameters (fraction of HF exchange) at short and long range''', respectively. | |||
*<math>\mu</math> is the '''screening parameter''' that determines the separation between short range (SR) and long range (LR). | |||
The SR and LR components of the full-range <math>E_{\mathrm{x}}^{\mathrm{SL}}</math> and <math>E_{\mathrm{x}}^{\mathrm{HF}}</math> exchange energies are constructed such that at all values of <math>\mu</math> | |||
*<math>E_{\mathrm{x}}^{\mathrm{HF}}=E_{\mathrm{x,SR}}^{\mathrm{HF}}(\mu)+E_{\mathrm{x,LR}}^{\mathrm{HF}}(\mu)</math> | |||
*<math>E_{\mathrm{x}}^{\mathrm{SL}}=E_{\mathrm{x,SR}}^{\mathrm{SL}}(\mu)+E_{\mathrm{x,LR}}^{\mathrm{SL}}(\mu)</math> | |||
The HF exchange energy (full-range, SR, or LR) is given by | |||
<span id="ExFockSR"> | |||
:<math> | :<math> | ||
E_{\mathrm{x,(SR/LR)}}^{\rm HF}(\mu)= | |||
-\frac{1}{2}\sum_{n\mathbf{k},m\mathbf{q}} | |||
f_{n\mathbf{k}} f_{m\mathbf{q}} | |||
\int \int d^3\mathbf{r} d^3\mathbf{r}' | |||
v(\mu,|\mathbf{r}-\mathbf{r}'|) | |||
\psi_{n\mathbf{k}}^{*}(\mathbf{r})\psi_{m\mathbf{q}}^{*}(\mathbf{r}') | |||
\psi_{n\mathbf{k}}(\mathbf{r}')\psi_{m\mathbf{q}}(\mathbf{r}) | |||
f_{n\mathbf{k}} f_{m\mathbf{q}} | |||
\int\int d^3\mathbf{r} d^3\mathbf{r}' | |||
\ | |||
\psi_{n\mathbf{k}}(\mathbf{r}')\psi_{m\mathbf{q}}(\mathbf{r}) | |||
</math> | </math> | ||
</span> | </span> | ||
with <math>\{\psi_{n\mathbf{k}}(\mathbf{r})\}</math> being the set of one-electron | with <math>\{\psi_{n\mathbf{k}}(\mathbf{r})\}</math> being the set of one-electron | ||
Bloch states of the system, and <math>\{f_{n\mathbf{k}}\}</math> the corresponding | Bloch states of the system, and <math>\{f_{n\mathbf{k}}\}</math> the corresponding | ||
set of (possibly fractional) occupational numbers. | set of (possibly fractional) occupational numbers. | ||
The sums over <math>{\bf k}</math> and <math>{\bf q}</math> run over all | The sums over <math>{\bf k}</math> and <math>{\bf q}</math> run over all k-points chosen to sample the Brillouin zone, whereas the sums over <math>m</math> and <math>n</math> run over all bands at these k-points. | ||
The corresponding nonlocal HF potential is given by | |||
<span id="VxFock"> | |||
:<math> | :<math> | ||
V_{\mathrm{x}}^{\mathrm{HF}}\left(\mathbf{r},\mathbf{r}'\right)= | V_{\mathrm{x,(SR/LR)}}^{\mathrm{HF}}\left(\mu,\mathbf{r},\mathbf{r}'\right)= | ||
- | -\sum_{m\mathbf{q}}f_{m\mathbf{q}}v(\mu,|\mathbf{r}-\mathbf{r}'|)\psi_{m\mathbf{q}}^{*}(\mathbf{r}')\psi_{m\mathbf{q}}(\mathbf{r}) | ||
</math> | </math> | ||
</span> | </span> | ||
The non-multiplicative form of the HF potential is such that hybrid functionals are implemented within the generalized KS scheme{{cite|seidl:prb:96}}. Thus, the total energy is minimized with respect to the orbitals (instead of the electron density), which means that the HF exchange leads to a nonlocal operator as in the Hartree-Fock-Roothaan theory. | |||
=== Expressions of Hartree-Fock energy and potential for the plane-wave basis set === | |||
Using the decomposition of the Bloch states <math>\psi_{m\mathbf{q}}</math> in plane waves, | |||
Using the decomposition of the Bloch states | |||
:<math> | :<math> | ||
| Line 73: | Line 46: | ||
</math> | </math> | ||
the | the HF exchange potential can be written as | ||
:<math> | :<math> | ||
V_{\mathrm{x}}^{\mathrm{HF}}\left(\mathbf{r},\mathbf{r}'\right)= | V_{\mathrm{x,(SR/LR)}}^{\mathrm{HF}}\left(\mu,\mathbf{r},\mathbf{r}'\right)= | ||
\sum_{\mathbf{k}}\sum_{\mathbf{G}\mathbf{G}'} | \sum_{\mathbf{k}}\sum_{\mathbf{G}\mathbf{G}'} | ||
e^{i(\mathbf{k}+\mathbf{G})\cdot\mathbf{r}} | e^{i(\mathbf{k}+\mathbf{G})\cdot\mathbf{r}} | ||
V_{\mathbf{k | V_{\mathbf{k}}\left(\mu, \mathbf{G},\mathbf{G}'\right) | ||
e^{-i(\mathbf{k}+\mathbf{G}')\cdot\mathbf{r}'} | e^{-i(\mathbf{k}+\mathbf{G}')\cdot\mathbf{r}'} | ||
</math> | </math> | ||
where | where | ||
:<math> | |||
V_{\mathbf{k}}\left(\mu, \mathbf{G},\mathbf{G}'\right)= | |||
\langle \mathbf{k}+\mathbf{G} | V_{\mathrm{x,(SR/LR)}}^{\mathrm{HF}} | \mathbf{k}+\mathbf{G}'\rangle | |||
</math> | |||
== Types of potentials == | |||
For most hybrid functionals proposed in the literature, the interelectronic Coulomb potential <math>v(\mu,|\mathbf{r}-\mathbf{r}'|)</math> is one of these types (<math>r=|\mathbf{r}-\mathbf{r}'|</math>): | |||
* Full range (bare Coulomb potential): | |||
:<math> | |||
v^{\mathrm{bare}}(r)=\frac{1}{r} | |||
</math> | |||
<span id="VxFockRecip"> | <span id="VxFockRecip"> | ||
:<math> | :<math> | ||
V_\mathbf{k}^{\mathrm{ | V_{\mathbf{k}}^{\mathrm{bare}}\left( \mathbf{G},\mathbf{G}'\right)= | ||
\ | -\frac{4\pi}{\Omega} \sum_{m\mathbf{q}}f_{m\mathbf{q}}\sum_{\mathbf{G}''} | ||
-\frac{4\pi | \frac{C^*_{m\mathbf{q}}(\mathbf{G}'-\mathbf{G}'') C_{m\mathbf{q}}(\mathbf{G}-\mathbf{G}'')} | ||
{|\mathbf{k}-\mathbf{q}+\mathbf{G}''|^2} | |||
</math> | |||
</span> | |||
* Short-range with error function: | |||
:<math> | |||
v_{\mathrm{SR}}^{\mathrm{erf}}(\mu,r)=\frac{\mathrm{erfc}(\mu r)}{r} | |||
</math> | |||
<span id="VxFockSRRecip"> | |||
:<math> | |||
\begin{align} | |||
V_{\mathbf{k},\mathrm{SR}}^{\mathrm{erf}}\left(\mu, \mathbf{G},\mathbf{G}'\right)= | |||
-\frac{4\pi}{\Omega} \sum_{m\mathbf{q}}f_{m\mathbf{q}}\sum_{\mathbf{G}''} | |||
\frac{C^*_{m\mathbf{q}}(\mathbf{G}'-\mathbf{G}'') C_{m\mathbf{q}}(\mathbf{G}-\mathbf{G}'')} | \frac{C^*_{m\mathbf{q}}(\mathbf{G}'-\mathbf{G}'') C_{m\mathbf{q}}(\mathbf{G}-\mathbf{G}'')} | ||
{|\mathbf{k}-\mathbf{q}+\mathbf{G}''|^2} | {|\mathbf{k}-\mathbf{q}+\mathbf{G}''|^2} | ||
\left( 1-e^{-|\mathbf{k}-\mathbf{q}+\mathbf{G}''|^2 /(4\mu^2)} \right) | |||
\end{align} | |||
</math> | |||
</span> | |||
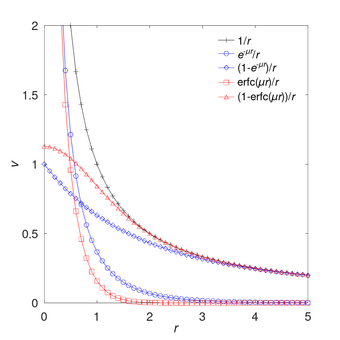
[[File:Screened_operator.png|340px|thumb|right|Short- and long-range potentials using the error or exponential screening compared to the bare potential. <math>\mu=1</math> is used.]] | |||
* Short-range with exponential function: | |||
:<math> | |||
v_{\mathrm{SR}}^{\mathrm{exp}}(\mu,r)=\frac{e^{-\mu r}}{r} | |||
</math> | |||
<span id="VxFockRecip"> | |||
:<math> | |||
V_{\mathbf{k},\mathrm{SR}}^{\mathrm{exp}}\left(\mu, \mathbf{G},\mathbf{G}'\right)= | |||
-\frac{4\pi}{\Omega} \sum_{m\mathbf{q}}f_{m\mathbf{q}}\sum_{\mathbf{G}''} | |||
\frac{C^*_{m\mathbf{q}}(\mathbf{G}'-\mathbf{G}'') C_{m\mathbf{q}}(\mathbf{G}-\mathbf{G}'')} | |||
{|\mathbf{k}-\mathbf{q}+\mathbf{G}''|^2 + \mu^2} | |||
</math> | </math> | ||
</span> | </span> | ||
The corresponding long-range potentials are given by <math>v_{\mathrm{LR}}^{\mathrm{erf/exp}}=v^{\mathrm{bare}}-v_{\mathrm{SR}}^{\mathrm{erf/exp}}</math>. | |||
In VASP, these expressions are implemented within the [[Projector-augmented-wave_formalism|PAW formalism]].{{cite|paier:jcp:05}} | In VASP, these expressions are implemented within the [[Projector-augmented-wave_formalism|PAW formalism]].{{cite|paier:jcp:05}} | ||
The families of hybrid functionals implemented in VASP are listed below along with examples, whose corresponding {{TAG|INCAR}} files can be found at the page [[list_of_hybrid_functionals|list of hybrid functionals]]. | |||
{{NB|important|The screening <math>\mu</math> ({{TAG|HFSCREEN}} tag) can be used only when the semilocal functional is PBE, PBEsol, or LDA ({{TAG|GGA}}{{=}}PE, PS, or CA, respectively). The other {{TAG|GGA}} and {{TAG|METAGGA}} functionals have no screened version available in VASP.}} | |||
== Families of hybrid functionals == | |||
=== | === HF exchange at full range === | ||
There is no range separation, i.e. the same fraction of HF exchange is applied at full range, <math>a_{\mathrm{SR}}=a_{\mathrm{LR}}=a</math> ({{TAG|AEXX}} tag): | |||
:<math>E_{\mathrm{xc}}^{\mathrm{hybrid}}=a E_{\mathrm{x}}^{\mathrm{HF}} + (1-a)E_{\mathrm{x}}^{\mathrm{SL}} + E_{\mathrm{c}}^{\mathrm{SL}}</math> | |||
{{NB|mind| | |||
*These functionals are set with {{TAG|LHFCALC}}{{=}}.TRUE. By default {{TAG|AEXX}}{{=}}0.25, but can be set to another value. | |||
*The semilocal part can be of the LDA, GGA or MGGA type. | |||
}} | |||
These are the original and most simple forms of hybrid functionals. Two examples, PBE0 and B3LYP, are given below. | |||
*[[list_of_hybrid_functionals#PBE0|PBE0]]:{{cite|perdew:jcp:1996}} | |||
:<math> | :<math> | ||
E_{\mathrm{xc}}^{\mathrm{ | E_{\mathrm{xc}}^{\mathrm{PBE0}}=\frac{1}{4} E_{\mathrm{x}}^{\mathrm{HF}} + | ||
\frac{3}{4} E_{\mathrm{x}}^{\mathrm{PBE}} + E_{\mathrm{c}}^{\mathrm{PBE}} | |||
</math> | </math> | ||
</span> | |||
:It is based on the PBE GGA functional{{cite|perdew:prl:1996}} and <math>a=1/4</math>. | |||
*[[list_of_hybrid_functionals#B3LYP|B3LYP]]{{cite|stephens:jpc:1994}}, well known and popular amongst quantum chemists: | |||
<span id=" | <span id="B3LYP"> | ||
:<math> | :<math> | ||
\ | \begin{align} | ||
E_{\mathrm{x}}^{\mathrm{B3LYP}} &=0.8 E_{\mathrm{x}}^{\mathrm{LDA}}+ | |||
0.2 E_{\mathrm{x}}^{\mathrm{HF}} + 0.72 (E_{\mathrm{x}}^{\mathrm{B88}}-E_{\mathrm{x}}^{\mathrm{LDA}}) + | |||
0.19 E_{\mathrm{c}}^{\mathrm{VWN3}}+ 0.81 E_{\mathrm{c}}^{\mathrm{LYP}} | |||
\end{align} | |||
</math> | </math> | ||
</span> | </span> | ||
:The exchange part consists of 80% of LDA exchange plus 20% of HF exchange, and 72% of the gradient corrections of the B88 GGA functional.{{cite|becke:pra:1988}} The correlation consists of 81% of LYP{{cite|lee:prb:1988}} correlation energy, which contains a LDA and a GGA part, and 19% of the LDA Vosko-Wilk-Nusair correlation functional III,{{cite|vosko1980}} which was fitted to the correlation energy in the random phase approximation of the homogeneous electron gas. | |||
=== HF exchange at short range (error-function screening) === | |||
The HF exchange is used only at short-range (the long-range part is fully semilocal, <math>a_{\mathrm{LR}}=0</math>) and the screening is done with the error function: | |||
:<math>E_{\mathrm{xc}}^{\mathrm{hybrid}}=a_{\mathrm{SR}} E_{\mathrm{x,SR}}^{\mathrm{HF}}(\mu) + (1-a_{\mathrm{SR}})E_{\mathrm{x,SR}}^{\mathrm{SL}}(\mu) + E_{\mathrm{x,LR}}^{\mathrm{SL}}(\mu) + E_{\mathrm{c}}^{\mathrm{SL}}</math> | |||
The mixing <math>a_{\mathrm{SR}}</math> and screening <math>\mu</math> are controlled by the {{TAG|AEXX}} and {{TAG|HFSCREEN}} tags, respectively. | |||
The most popular range-separated functional, HSE, is given below. | |||
*[[List_of_hybrid_functionals#HSE03|HSE03]]{{cite|heyd:jcp:03}}{{cite|heyd:jcp:04}}{{cite|heyd:jcp:06}} and [[List_of_hybrid_functionals#HSE06|HSE06]]{{cite|krukau:jcp:06}}: | |||
:<math> | |||
E_{\mathrm{xc}}^{\mathrm{HSE}}= \frac{1}{4}E_{\mathrm{x,SR}}^{\mathrm{HF}}(\mu) | |||
+ \frac{3}{4} E_{\mathrm{x,SR}}^{\mathrm{PBE}}(\mu) | |||
+ E_{\mathrm{x,LR}}^{\mathrm{PBE}}(\mu) + E_{\mathrm{c}}^{\mathrm{PBE}} | |||
</math> | |||
:They are based on the PBE GGA functional{{cite|perdew:prl:1996}} and <math>a_{\mathrm{SR}}=1/4</math>. It has been shown that the optimum <math>\mu</math>, controlling the range separation is approximately 0.2-0.3 Å<sup>-1</sup>.{{cite|heyd:jcp:03}}{{cite|heyd:jcp:04}}{{cite|heyd:jcp:06}}{{cite|krukau:jcp:06}} [[List_of_hybrid_functionals#HSE03|HSE03]] and [[List_of_hybrid_functionals#HSE06|HSE06]] correspond to {{TAG|HFSCREEN}}=0.3 and 0.2, respectively. Note that the two limit cases of HSE are [[List_of_hybrid_functionals#PBE0|PBE0]] at <math>\mu=0</math> and PBE at <math>\mu\rightarrow\infty</math>. | |||
=== HF exchange at short range and long range (error-function screening) with different mixings === | |||
The fractions of HF exchange at short and long range (<math>a_{\mathrm{SR}}</math> and <math>a_{\mathrm{LR}}</math>, respectively) can be different: | |||
:<math>E_{\mathrm{xc}}^{\mathrm{hybrid}}=a_{\mathrm{SR}} E_{\mathrm{x,SR}}^{\mathrm{HF}}(\mu) + a_{\mathrm{LR}} E_{\mathrm{x,LR}}^{\mathrm{HF}}(\mu) + (1-a_{\mathrm{SR}})E_{\mathrm{x,SR}}^{\mathrm{SL}}(\mu) + (1-a_{\mathrm{LR}})E_{\mathrm{x,LR}}^{\mathrm{SL}}(\mu) + E_{\mathrm{c}}^{\mathrm{SL}}</math> | |||
These functionals are selected with {{TAG|LMODELHF}}=.TRUE. The mixings <math>a_{\mathrm{LR}}</math> and <math>a_{\mathrm{SR}}</math> are controlled by the {{TAG|AEXX}} and {{TAG|BEXX}} tags, respectively, and the screening <math>\mu</math> by the {{TAG|HFSCREEN}} tag. | |||
{{NB|important|The possibility to set <math>a_{\mathrm{SR}}</math> with {{TAG|BEXX}} within the {{TAG|LMODELHF}}{{=}}.TRUE. method was introduced in VASP.6.6.0. Until VASP.6.5.1 <math>a_{\mathrm{SR}}</math> was fixed to 1 and could not be changed.}} | |||
This functional form has been used in the context of dielectric-dependent hybrids. Examples are provided below. | |||
*[[List_of_hybrid_functionals#RS-DDH|RS-DDH]]:{{cite|skone:prb:2016}} | |||
:<math> | :<math> | ||
E_{\mathrm{xc}}^{\mathrm{RS-DDH}}=\frac{1}{4} E_{\mathrm{x,SR}}^{\mathrm{HF}}(\mu) + a_{\mathrm{LR}} E_{\mathrm{x,LR}}^{\mathrm{HF}}(\mu) + \frac{3}{4}E_{\mathrm{x,SR}}^{\mathrm{PBE}}(\mu) + (1-a_{\mathrm{LR}})E_{\mathrm{x,LR}}^{\mathrm{PBE}}(\mu) + E_{\mathrm{c}}^{\mathrm{PBE}} | |||
\ | |||
</math> | </math> | ||
</ | :where <math>a_{\mathrm{SR}}=1/4</math> and <math>a_{\mathrm{LR}}=\varepsilon^{-1}</math> is chosen as the inverse of the dielectric constant <math>\varepsilon^{-1}</math>. | ||
*[[List_of_hybrid_functionals#DD-RSH-CAM|DD-RSH-CAM]],{{cite|chen2018nonempirical}} [[List_of_hybrid_functionals#DD-RSH-CAM|DSH]]:{{cite|cui2018doubly}} | |||
:<math> | :<math> | ||
E_{\mathrm{xc}}^{\mathrm{DD-RSH-CAM}}=E_{\mathrm{x,SR}}^{\mathrm{HF}}(\mu) + a_{\mathrm{LR}} E_{\mathrm{x,LR}}^{\mathrm{HF}}(\mu) + (1-a_{\mathrm{LR}})E_{\mathrm{x,LR}}^{\mathrm{PBE}}(\mu) + E_{\mathrm{c}}^{\mathrm{PBE}} | |||
</math> | </math> | ||
</ | :where <math>a_{\mathrm{SR}}=1</math> and <math>a_{\mathrm{LR}}=\varepsilon^{-1}</math> is chosen as the inverse of the dielectric constant <math>\varepsilon^{-1}</math>. | ||
=== HF exchange at long range (error-function screening) === | |||
The | The HF exchange is used only at long-range (the short-range part is fully semilocal, <math>a_{\mathrm{SR}}=0</math>) and the screening is done with the error function: | ||
< | :<math>E_{\mathrm{xc}}^{\mathrm{hybrid}}=a_{\mathrm{LR}} E_{\mathrm{x,LR}}^{\mathrm{HF}}(\mu) + E_{\mathrm{x,SR}}^{\mathrm{SL}}(\mu) + (1-a_{\mathrm{LR}})E_{\mathrm{x,LR}}^{\mathrm{SL}}(\mu) + E_{\mathrm{c}}^{\mathrm{SL}}</math> | ||
==== | These functionals are selected with {{TAG|LRHFCALC}}=.TRUE. The mixing <math>a_{\mathrm{LR}}</math> and screening <math>\mu</math> are controlled by the {{TAG|AEXX}} and {{TAG|HFSCREEN}} tags, respectively. | ||
{{NB|mind|{{TAG|LRHFCALC}}{{=}}.TRUE. automatically sets {{TAG|AEXX}}{{=}}1. However, {{TAG|AEXX}} can be set to another value.}} | |||
{{NB|important|When {{TAG|AEXX}}{{=}}1 (the default for {{TAG|LRHFCALC}}{{=}}.TRUE.), the correlation <math>E_{\mathrm{c}}^{\mathrm{SL}}</math> is not included. However, it can be included by setting {{TAG|ALDAC}}{{=}}1.0 and {{TAG|AGGAC}}{{=}}1.0.}} | |||
Long-range hybrid functionals are more popular in molecular chemistry, where a proper decay of the exchange-correlation potential at long range far from the nuclei may be important, and thus less useful for bulk solids. Examples belonging to this class of functionals are: | |||
*[[List_of_hybrid_functionals#RSHXLDA|RSHXLDA]] and [[List_of_hybrid_functionals#RSHXPBE|RSHXPBE]]:{{cite|iikura:jcp:2001}}{{cite|gerber:cpl:2005}}{{cite|gerber:jcp:2007}} | *[[List_of_hybrid_functionals#RSHXLDA|RSHXLDA]] and [[List_of_hybrid_functionals#RSHXPBE|RSHXPBE]]:{{cite|iikura:jcp:2001}}{{cite|gerber:cpl:2005}}{{cite|gerber:jcp:2007}} | ||
:<math> | :<math> | ||
E_{\mathrm{xc}}^{\mathrm{RSHXLDA}}= E_{\mathrm{x}}^{\mathrm{ | E_{\mathrm{xc}}^{\mathrm{RSHXLDA}} = E_{\mathrm{x,LR}}^{\mathrm{HF}}(\mu) + E_{\mathrm{x,SR}}^{\mathrm{LDA}}(\mu) + E_{\mathrm{c}}^{\mathrm{LDA}} | ||
+ E_{\mathrm{x}}^{\mathrm{ | |||
</math> | </math> | ||
:<math> | :<math> | ||
E_{\mathrm{xc}}^{\mathrm{RSHXPBE}}= E_{\mathrm{x}}^{\mathrm{ | E_{\mathrm{xc}}^{\mathrm{RSHXPBE}} = E_{\mathrm{x,LR}}^{\mathrm{HF}}(\mu) + E_{\mathrm{x,SR}}^{\mathrm{PBE}}(\mu) + E_{\mathrm{c}}^{\mathrm{PBE}} | ||
+ E_{\mathrm{x}}^{\mathrm{ | |||
</math> | </math> | ||
: | :When LDA is chosen, a value of <math>\mu=0.75</math> Å<sup>-1</sup> is recommended for solids.{{cite|gerber:jcp:2007}} | ||
=== | === HF exchange at short range (exponential screening) === | ||
< | The HF exchange is used only at short-range (the long-range part is fully semilocal, <math>a_{\mathrm{LR}}=0</math>) and the screening is done with the exponential function: | ||
:<math>E_{\mathrm{xc}}^{\mathrm{hybrid}}=a_{\mathrm{SR}} E_{\mathrm{x,SR}}^{\mathrm{HF}}(\mu) + (1-a_{\mathrm{SR}})E_{\mathrm{x,SR}}^{\mathrm{SL}}(\mu) + E_{\mathrm{x,LR}}^{\mathrm{SL}}(\mu) + E_{\mathrm{c}}^{\mathrm{SL}}</math> | |||
The exponential screening, also called Thomas-Fermi (TF) screening,{{cite|bylander:prb:90}}{{cite|seidl:prb:96}}{{cite|picozzi:prb:00}} is activated by setting {{TAG|LTHOMAS}}=.TRUE.. The mixing <math>a_{\mathrm{SR}}</math> and screening <math>\mu=k_{\rm TF}</math> are controlled by the {{TAG|AEXX}} and {{TAG|HFSCREEN}} tags, respectively. | |||
{{NB|mind|{{TAG|LTHOMAS}}{{=}}.TRUE. automatically sets {{TAG|AEXX}}{{=}}1. However, {{TAG|AEXX}} can be set to another value.}} | |||
{{NB|important| | |||
*When {{TAG|AEXX}}{{=}}1 (the default for {{TAG|LTHOMAS}}{{=}}.TRUE.), the correlation <math>E_{\mathrm{c}}^{\mathrm{SL}}</math> is not included. However, it can be included by setting {{TAG|ALDAC}}{{=}}1.0 and {{TAG|AGGAC}}{{=}}1.0. | |||
*This functional should be used only with LDA ({{TAG|GGA}}{{=}}CA).}} | |||
The sX-LDA functional, which uses <math>a_{\mathrm{SR}}=1</math>, is probably the first hybrid using an exponential screening: | |||
*[[List_of_hybrid_functionals#sX-LDA|sX-LDA]]:{{cite|bylander:prb:90}} | |||
:<math> | :<math> | ||
\ | E_{\mathrm{xc}}^{\mathrm{sX-LDA}} = E_{\mathrm{x,SR}}^{\mathrm{HF}}(\mu) + E_{\mathrm{x,LR}}^{\mathrm{LDA}}(\mu) + E_{\mathrm{c}}^{\mathrm{LDA}} | ||
</math> | </math> | ||
For typical semiconductors, a Thomas-Fermi screening length <math>\mu=k_{\rm TF}</math> of about 1.8 Å<sup>-1</sup> yields reasonable band gaps. In principle, however, the Thomas-Fermi screening length depends on the valence-electron density. VASP determines <math>k_{\rm TF}</math> from the number of valence electrons (read from the {{FILE|POTCAR}} file) and the volume (leading to an average density <math>\bar{n}</math>) and writes the corresponding value of <math>k_{\rm TF}=\sqrt{4\bar{k}_{\rm F}/\pi}</math>, where <math>\bar{k}_{\rm F}=(3\pi^2\bar{n})^{1/3}</math> to the {{FILE|OUTCAR}} file ('''note that this value is only printed for information and is not used during the calculation'''): | |||
Thomas-Fermi vector in A = 2.00000 | Thomas-Fermi vector in A = 2.00000 | ||
Since VASP counts the semi-core states and ''d''-states as valence electrons, although these states do not contribute to the screening, the values reported by VASP are often | Since VASP counts the semi-core states and ''d''-states as valence electrons, although these states do not contribute to the screening, the values reported by VASP are often not recommended. | ||
Another important detail concerns the implementation of the | Another important detail concerns the implementation of the local LDA part in VASP. Literature [see Eqs. (3.10), (3.14), and (3.15) in Ref. {{cite|seidl:prb:96}}] suggests to use in the enhancement factor <math>F(z)</math> a position-independent variable <math>z=k_{\rm TF}/\bar{k}_{\rm F}</math> where <math>\bar{k}_{\rm F}</math> is as defined above but using the average density <math>\bar{n}</math> in the unit cell. | ||
However, implemented in VASP is a position-dependent variable <math>z({\bf r})=k_{\rm TF}/k_{\rm F}({\bf r})</math>, where <math>k_{\rm F}({\bf r})=(3\pi^2 n({\bf r}))^{1/3}</math> is the Fermi wave vector calculated with the local density <math>n({\bf r})</math>, while the constant <math>k_{\rm TF}</math> is set by {{TAG|HFSCREEN}}. | |||
== Related tags and articles == | == Related tags and articles == | ||
{{TAG|AEXX}}, | {{TAG|AEXX}}, | ||
{{TAG|BEXX}}, | |||
{{TAG|ALDAX}}, | {{TAG|ALDAX}}, | ||
{{TAG|ALDAC}}, | {{TAG|ALDAC}}, | ||
| Line 203: | Line 247: | ||
{{TAG|AMGGAX}}, | {{TAG|AMGGAX}}, | ||
{{TAG|AMGGAC}}, | {{TAG|AMGGAC}}, | ||
{{TAG|HFSCREEN}}, | |||
{{TAG|LHFCALC}}, | {{TAG|LHFCALC}}, | ||
{{TAG|LMODELHF}}, | {{TAG|LMODELHF}}, | ||
{{TAG|LTHOMAS}}, | {{TAG|LTHOMAS}}, | ||
{{TAG|LRHFCALC}}, | {{TAG|LRHFCALC}}, | ||
[[List of hybrid functionals]], | [[List of hybrid functionals]], | ||
[[Downsampling of the Hartree-Fock operator]], | [[Downsampling of the Hartree-Fock operator]], | ||
Latest revision as of 22:18, 27 February 2026
The exchange energy in hybrid functionals is a mixture of semilocal (SL) and nonlocal Hartree-Fock (HF) types. They can be categorized into different families according to the type of semilocal approximation (LDA, GGA, or MGGA) or the treatment of the short- and long-range parts of the exchange. A rather general formula that encompasses the different families of hybrid functionals is given by
- [math]\displaystyle{ E_{\mathrm{xc}}^{\mathrm{hybrid}}=a_{\mathrm{SR}} E_{\mathrm{x,SR}}^{\mathrm{HF}}(\mu) + a_{\mathrm{LR}} E_{\mathrm{x,LR}}^{\mathrm{HF}}(\mu) + (1-a_{\mathrm{SR}})E_{\mathrm{x,SR}}^{\mathrm{SL}}(\mu) + (1-a_{\mathrm{LR}})E_{\mathrm{x,LR}}^{\mathrm{SL}}(\mu) + E_{\mathrm{c}}^{\mathrm{SL}} }[/math]
where
- [math]\displaystyle{ a_{\mathrm{SR}} }[/math] and [math]\displaystyle{ a_{\mathrm{LR}} }[/math] are the mixing parameters (fraction of HF exchange) at short and long range, respectively.
- [math]\displaystyle{ \mu }[/math] is the screening parameter that determines the separation between short range (SR) and long range (LR).
The SR and LR components of the full-range [math]\displaystyle{ E_{\mathrm{x}}^{\mathrm{SL}} }[/math] and [math]\displaystyle{ E_{\mathrm{x}}^{\mathrm{HF}} }[/math] exchange energies are constructed such that at all values of [math]\displaystyle{ \mu }[/math]
- [math]\displaystyle{ E_{\mathrm{x}}^{\mathrm{HF}}=E_{\mathrm{x,SR}}^{\mathrm{HF}}(\mu)+E_{\mathrm{x,LR}}^{\mathrm{HF}}(\mu) }[/math]
- [math]\displaystyle{ E_{\mathrm{x}}^{\mathrm{SL}}=E_{\mathrm{x,SR}}^{\mathrm{SL}}(\mu)+E_{\mathrm{x,LR}}^{\mathrm{SL}}(\mu) }[/math]
The HF exchange energy (full-range, SR, or LR) is given by
- [math]\displaystyle{ E_{\mathrm{x,(SR/LR)}}^{\rm HF}(\mu)= -\frac{1}{2}\sum_{n\mathbf{k},m\mathbf{q}} f_{n\mathbf{k}} f_{m\mathbf{q}} \int \int d^3\mathbf{r} d^3\mathbf{r}' v(\mu,|\mathbf{r}-\mathbf{r}'|) \psi_{n\mathbf{k}}^{*}(\mathbf{r})\psi_{m\mathbf{q}}^{*}(\mathbf{r}') \psi_{n\mathbf{k}}(\mathbf{r}')\psi_{m\mathbf{q}}(\mathbf{r}) }[/math]
with [math]\displaystyle{ \{\psi_{n\mathbf{k}}(\mathbf{r})\} }[/math] being the set of one-electron Bloch states of the system, and [math]\displaystyle{ \{f_{n\mathbf{k}}\} }[/math] the corresponding set of (possibly fractional) occupational numbers. The sums over [math]\displaystyle{ {\bf k} }[/math] and [math]\displaystyle{ {\bf q} }[/math] run over all k-points chosen to sample the Brillouin zone, whereas the sums over [math]\displaystyle{ m }[/math] and [math]\displaystyle{ n }[/math] run over all bands at these k-points. The corresponding nonlocal HF potential is given by
- [math]\displaystyle{ V_{\mathrm{x,(SR/LR)}}^{\mathrm{HF}}\left(\mu,\mathbf{r},\mathbf{r}'\right)= -\sum_{m\mathbf{q}}f_{m\mathbf{q}}v(\mu,|\mathbf{r}-\mathbf{r}'|)\psi_{m\mathbf{q}}^{*}(\mathbf{r}')\psi_{m\mathbf{q}}(\mathbf{r}) }[/math]
The non-multiplicative form of the HF potential is such that hybrid functionals are implemented within the generalized KS scheme[1]. Thus, the total energy is minimized with respect to the orbitals (instead of the electron density), which means that the HF exchange leads to a nonlocal operator as in the Hartree-Fock-Roothaan theory.
Expressions of Hartree-Fock energy and potential for the plane-wave basis set
Using the decomposition of the Bloch states [math]\displaystyle{ \psi_{m\mathbf{q}} }[/math] in plane waves,
- [math]\displaystyle{ \psi_{m\mathbf{q}}(\mathbf{r})= \frac{1}{\sqrt{\Omega}} \sum_\mathbf{G}C_{m\mathbf{q}}(\mathbf{G})e^{i(\mathbf{q}+\mathbf{G}) \cdot \mathbf{r}} }[/math]
the HF exchange potential can be written as
- [math]\displaystyle{ V_{\mathrm{x,(SR/LR)}}^{\mathrm{HF}}\left(\mu,\mathbf{r},\mathbf{r}'\right)= \sum_{\mathbf{k}}\sum_{\mathbf{G}\mathbf{G}'} e^{i(\mathbf{k}+\mathbf{G})\cdot\mathbf{r}} V_{\mathbf{k}}\left(\mu, \mathbf{G},\mathbf{G}'\right) e^{-i(\mathbf{k}+\mathbf{G}')\cdot\mathbf{r}'} }[/math]
where
- [math]\displaystyle{ V_{\mathbf{k}}\left(\mu, \mathbf{G},\mathbf{G}'\right)= \langle \mathbf{k}+\mathbf{G} | V_{\mathrm{x,(SR/LR)}}^{\mathrm{HF}} | \mathbf{k}+\mathbf{G}'\rangle }[/math]
Types of potentials
For most hybrid functionals proposed in the literature, the interelectronic Coulomb potential [math]\displaystyle{ v(\mu,|\mathbf{r}-\mathbf{r}'|) }[/math] is one of these types ([math]\displaystyle{ r=|\mathbf{r}-\mathbf{r}'| }[/math]):
- Full range (bare Coulomb potential):
- [math]\displaystyle{ v^{\mathrm{bare}}(r)=\frac{1}{r} }[/math]
- [math]\displaystyle{ V_{\mathbf{k}}^{\mathrm{bare}}\left( \mathbf{G},\mathbf{G}'\right)= -\frac{4\pi}{\Omega} \sum_{m\mathbf{q}}f_{m\mathbf{q}}\sum_{\mathbf{G}''} \frac{C^*_{m\mathbf{q}}(\mathbf{G}'-\mathbf{G}'') C_{m\mathbf{q}}(\mathbf{G}-\mathbf{G}'')} {|\mathbf{k}-\mathbf{q}+\mathbf{G}''|^2} }[/math]
- Short-range with error function:
- [math]\displaystyle{ v_{\mathrm{SR}}^{\mathrm{erf}}(\mu,r)=\frac{\mathrm{erfc}(\mu r)}{r} }[/math]
- [math]\displaystyle{ \begin{align} V_{\mathbf{k},\mathrm{SR}}^{\mathrm{erf}}\left(\mu, \mathbf{G},\mathbf{G}'\right)= -\frac{4\pi}{\Omega} \sum_{m\mathbf{q}}f_{m\mathbf{q}}\sum_{\mathbf{G}''} \frac{C^*_{m\mathbf{q}}(\mathbf{G}'-\mathbf{G}'') C_{m\mathbf{q}}(\mathbf{G}-\mathbf{G}'')} {|\mathbf{k}-\mathbf{q}+\mathbf{G}''|^2} \left( 1-e^{-|\mathbf{k}-\mathbf{q}+\mathbf{G}''|^2 /(4\mu^2)} \right) \end{align} }[/math]
- Short-range with exponential function:
- [math]\displaystyle{ v_{\mathrm{SR}}^{\mathrm{exp}}(\mu,r)=\frac{e^{-\mu r}}{r} }[/math]
- [math]\displaystyle{ V_{\mathbf{k},\mathrm{SR}}^{\mathrm{exp}}\left(\mu, \mathbf{G},\mathbf{G}'\right)= -\frac{4\pi}{\Omega} \sum_{m\mathbf{q}}f_{m\mathbf{q}}\sum_{\mathbf{G}''} \frac{C^*_{m\mathbf{q}}(\mathbf{G}'-\mathbf{G}'') C_{m\mathbf{q}}(\mathbf{G}-\mathbf{G}'')} {|\mathbf{k}-\mathbf{q}+\mathbf{G}''|^2 + \mu^2} }[/math]
The corresponding long-range potentials are given by [math]\displaystyle{ v_{\mathrm{LR}}^{\mathrm{erf/exp}}=v^{\mathrm{bare}}-v_{\mathrm{SR}}^{\mathrm{erf/exp}} }[/math].
In VASP, these expressions are implemented within the PAW formalism.[2]
The families of hybrid functionals implemented in VASP are listed below along with examples, whose corresponding INCAR files can be found at the page list of hybrid functionals.
| Important: The screening [math]\displaystyle{ \mu }[/math] (HFSCREEN tag) can be used only when the semilocal functional is PBE, PBEsol, or LDA (GGA=PE, PS, or CA, respectively). The other GGA and METAGGA functionals have no screened version available in VASP. |
Families of hybrid functionals
HF exchange at full range
There is no range separation, i.e. the same fraction of HF exchange is applied at full range, [math]\displaystyle{ a_{\mathrm{SR}}=a_{\mathrm{LR}}=a }[/math] (AEXX tag):
- [math]\displaystyle{ E_{\mathrm{xc}}^{\mathrm{hybrid}}=a E_{\mathrm{x}}^{\mathrm{HF}} + (1-a)E_{\mathrm{x}}^{\mathrm{SL}} + E_{\mathrm{c}}^{\mathrm{SL}} }[/math]
| Mind: |
These are the original and most simple forms of hybrid functionals. Two examples, PBE0 and B3LYP, are given below.
- [math]\displaystyle{ E_{\mathrm{xc}}^{\mathrm{PBE0}}=\frac{1}{4} E_{\mathrm{x}}^{\mathrm{HF}} + \frac{3}{4} E_{\mathrm{x}}^{\mathrm{PBE}} + E_{\mathrm{c}}^{\mathrm{PBE}} }[/math]
- It is based on the PBE GGA functional[4] and [math]\displaystyle{ a=1/4 }[/math].
- [math]\displaystyle{ \begin{align} E_{\mathrm{x}}^{\mathrm{B3LYP}} &=0.8 E_{\mathrm{x}}^{\mathrm{LDA}}+ 0.2 E_{\mathrm{x}}^{\mathrm{HF}} + 0.72 (E_{\mathrm{x}}^{\mathrm{B88}}-E_{\mathrm{x}}^{\mathrm{LDA}}) + 0.19 E_{\mathrm{c}}^{\mathrm{VWN3}}+ 0.81 E_{\mathrm{c}}^{\mathrm{LYP}} \end{align} }[/math]
- The exchange part consists of 80% of LDA exchange plus 20% of HF exchange, and 72% of the gradient corrections of the B88 GGA functional.[6] The correlation consists of 81% of LYP[7] correlation energy, which contains a LDA and a GGA part, and 19% of the LDA Vosko-Wilk-Nusair correlation functional III,[8] which was fitted to the correlation energy in the random phase approximation of the homogeneous electron gas.
HF exchange at short range (error-function screening)
The HF exchange is used only at short-range (the long-range part is fully semilocal, [math]\displaystyle{ a_{\mathrm{LR}}=0 }[/math]) and the screening is done with the error function:
- [math]\displaystyle{ E_{\mathrm{xc}}^{\mathrm{hybrid}}=a_{\mathrm{SR}} E_{\mathrm{x,SR}}^{\mathrm{HF}}(\mu) + (1-a_{\mathrm{SR}})E_{\mathrm{x,SR}}^{\mathrm{SL}}(\mu) + E_{\mathrm{x,LR}}^{\mathrm{SL}}(\mu) + E_{\mathrm{c}}^{\mathrm{SL}} }[/math]
The mixing [math]\displaystyle{ a_{\mathrm{SR}} }[/math] and screening [math]\displaystyle{ \mu }[/math] are controlled by the AEXX and HFSCREEN tags, respectively.
The most popular range-separated functional, HSE, is given below.
- [math]\displaystyle{ E_{\mathrm{xc}}^{\mathrm{HSE}}= \frac{1}{4}E_{\mathrm{x,SR}}^{\mathrm{HF}}(\mu) + \frac{3}{4} E_{\mathrm{x,SR}}^{\mathrm{PBE}}(\mu) + E_{\mathrm{x,LR}}^{\mathrm{PBE}}(\mu) + E_{\mathrm{c}}^{\mathrm{PBE}} }[/math]
- They are based on the PBE GGA functional[4] and [math]\displaystyle{ a_{\mathrm{SR}}=1/4 }[/math]. It has been shown that the optimum [math]\displaystyle{ \mu }[/math], controlling the range separation is approximately 0.2-0.3 Å-1.[9][10][11][12] HSE03 and HSE06 correspond to HFSCREEN=0.3 and 0.2, respectively. Note that the two limit cases of HSE are PBE0 at [math]\displaystyle{ \mu=0 }[/math] and PBE at [math]\displaystyle{ \mu\rightarrow\infty }[/math].
HF exchange at short range and long range (error-function screening) with different mixings
The fractions of HF exchange at short and long range ([math]\displaystyle{ a_{\mathrm{SR}} }[/math] and [math]\displaystyle{ a_{\mathrm{LR}} }[/math], respectively) can be different:
- [math]\displaystyle{ E_{\mathrm{xc}}^{\mathrm{hybrid}}=a_{\mathrm{SR}} E_{\mathrm{x,SR}}^{\mathrm{HF}}(\mu) + a_{\mathrm{LR}} E_{\mathrm{x,LR}}^{\mathrm{HF}}(\mu) + (1-a_{\mathrm{SR}})E_{\mathrm{x,SR}}^{\mathrm{SL}}(\mu) + (1-a_{\mathrm{LR}})E_{\mathrm{x,LR}}^{\mathrm{SL}}(\mu) + E_{\mathrm{c}}^{\mathrm{SL}} }[/math]
These functionals are selected with LMODELHF=.TRUE. The mixings [math]\displaystyle{ a_{\mathrm{LR}} }[/math] and [math]\displaystyle{ a_{\mathrm{SR}} }[/math] are controlled by the AEXX and BEXX tags, respectively, and the screening [math]\displaystyle{ \mu }[/math] by the HFSCREEN tag.
| Important: The possibility to set [math]\displaystyle{ a_{\mathrm{SR}} }[/math] with BEXX within the LMODELHF=.TRUE. method was introduced in VASP.6.6.0. Until VASP.6.5.1 [math]\displaystyle{ a_{\mathrm{SR}} }[/math] was fixed to 1 and could not be changed. |
This functional form has been used in the context of dielectric-dependent hybrids. Examples are provided below.
- [math]\displaystyle{ E_{\mathrm{xc}}^{\mathrm{RS-DDH}}=\frac{1}{4} E_{\mathrm{x,SR}}^{\mathrm{HF}}(\mu) + a_{\mathrm{LR}} E_{\mathrm{x,LR}}^{\mathrm{HF}}(\mu) + \frac{3}{4}E_{\mathrm{x,SR}}^{\mathrm{PBE}}(\mu) + (1-a_{\mathrm{LR}})E_{\mathrm{x,LR}}^{\mathrm{PBE}}(\mu) + E_{\mathrm{c}}^{\mathrm{PBE}} }[/math]
- where [math]\displaystyle{ a_{\mathrm{SR}}=1/4 }[/math] and [math]\displaystyle{ a_{\mathrm{LR}}=\varepsilon^{-1} }[/math] is chosen as the inverse of the dielectric constant [math]\displaystyle{ \varepsilon^{-1} }[/math].
- [math]\displaystyle{ E_{\mathrm{xc}}^{\mathrm{DD-RSH-CAM}}=E_{\mathrm{x,SR}}^{\mathrm{HF}}(\mu) + a_{\mathrm{LR}} E_{\mathrm{x,LR}}^{\mathrm{HF}}(\mu) + (1-a_{\mathrm{LR}})E_{\mathrm{x,LR}}^{\mathrm{PBE}}(\mu) + E_{\mathrm{c}}^{\mathrm{PBE}} }[/math]
- where [math]\displaystyle{ a_{\mathrm{SR}}=1 }[/math] and [math]\displaystyle{ a_{\mathrm{LR}}=\varepsilon^{-1} }[/math] is chosen as the inverse of the dielectric constant [math]\displaystyle{ \varepsilon^{-1} }[/math].
HF exchange at long range (error-function screening)
The HF exchange is used only at long-range (the short-range part is fully semilocal, [math]\displaystyle{ a_{\mathrm{SR}}=0 }[/math]) and the screening is done with the error function:
- [math]\displaystyle{ E_{\mathrm{xc}}^{\mathrm{hybrid}}=a_{\mathrm{LR}} E_{\mathrm{x,LR}}^{\mathrm{HF}}(\mu) + E_{\mathrm{x,SR}}^{\mathrm{SL}}(\mu) + (1-a_{\mathrm{LR}})E_{\mathrm{x,LR}}^{\mathrm{SL}}(\mu) + E_{\mathrm{c}}^{\mathrm{SL}} }[/math]
These functionals are selected with LRHFCALC=.TRUE. The mixing [math]\displaystyle{ a_{\mathrm{LR}} }[/math] and screening [math]\displaystyle{ \mu }[/math] are controlled by the AEXX and HFSCREEN tags, respectively.
| Mind: LRHFCALC=.TRUE. automatically sets AEXX=1. However, AEXX can be set to another value. |
| Important: When AEXX=1 (the default for LRHFCALC=.TRUE.), the correlation [math]\displaystyle{ E_{\mathrm{c}}^{\mathrm{SL}} }[/math] is not included. However, it can be included by setting ALDAC=1.0 and AGGAC=1.0. |
Long-range hybrid functionals are more popular in molecular chemistry, where a proper decay of the exchange-correlation potential at long range far from the nuclei may be important, and thus less useful for bulk solids. Examples belonging to this class of functionals are:
- [math]\displaystyle{ E_{\mathrm{xc}}^{\mathrm{RSHXLDA}} = E_{\mathrm{x,LR}}^{\mathrm{HF}}(\mu) + E_{\mathrm{x,SR}}^{\mathrm{LDA}}(\mu) + E_{\mathrm{c}}^{\mathrm{LDA}} }[/math]
- [math]\displaystyle{ E_{\mathrm{xc}}^{\mathrm{RSHXPBE}} = E_{\mathrm{x,LR}}^{\mathrm{HF}}(\mu) + E_{\mathrm{x,SR}}^{\mathrm{PBE}}(\mu) + E_{\mathrm{c}}^{\mathrm{PBE}} }[/math]
- When LDA is chosen, a value of [math]\displaystyle{ \mu=0.75 }[/math] Å-1 is recommended for solids.[18]
HF exchange at short range (exponential screening)
The HF exchange is used only at short-range (the long-range part is fully semilocal, [math]\displaystyle{ a_{\mathrm{LR}}=0 }[/math]) and the screening is done with the exponential function:
- [math]\displaystyle{ E_{\mathrm{xc}}^{\mathrm{hybrid}}=a_{\mathrm{SR}} E_{\mathrm{x,SR}}^{\mathrm{HF}}(\mu) + (1-a_{\mathrm{SR}})E_{\mathrm{x,SR}}^{\mathrm{SL}}(\mu) + E_{\mathrm{x,LR}}^{\mathrm{SL}}(\mu) + E_{\mathrm{c}}^{\mathrm{SL}} }[/math]
The exponential screening, also called Thomas-Fermi (TF) screening,[19][1][20] is activated by setting LTHOMAS=.TRUE.. The mixing [math]\displaystyle{ a_{\mathrm{SR}} }[/math] and screening [math]\displaystyle{ \mu=k_{\rm TF} }[/math] are controlled by the AEXX and HFSCREEN tags, respectively.
| Mind: LTHOMAS=.TRUE. automatically sets AEXX=1. However, AEXX can be set to another value. |
| Important: |
The sX-LDA functional, which uses [math]\displaystyle{ a_{\mathrm{SR}}=1 }[/math], is probably the first hybrid using an exponential screening:
- [math]\displaystyle{ E_{\mathrm{xc}}^{\mathrm{sX-LDA}} = E_{\mathrm{x,SR}}^{\mathrm{HF}}(\mu) + E_{\mathrm{x,LR}}^{\mathrm{LDA}}(\mu) + E_{\mathrm{c}}^{\mathrm{LDA}} }[/math]
For typical semiconductors, a Thomas-Fermi screening length [math]\displaystyle{ \mu=k_{\rm TF} }[/math] of about 1.8 Å-1 yields reasonable band gaps. In principle, however, the Thomas-Fermi screening length depends on the valence-electron density. VASP determines [math]\displaystyle{ k_{\rm TF} }[/math] from the number of valence electrons (read from the POTCAR file) and the volume (leading to an average density [math]\displaystyle{ \bar{n} }[/math]) and writes the corresponding value of [math]\displaystyle{ k_{\rm TF}=\sqrt{4\bar{k}_{\rm F}/\pi} }[/math], where [math]\displaystyle{ \bar{k}_{\rm F}=(3\pi^2\bar{n})^{1/3} }[/math] to the OUTCAR file (note that this value is only printed for information and is not used during the calculation):
Thomas-Fermi vector in A = 2.00000
Since VASP counts the semi-core states and d-states as valence electrons, although these states do not contribute to the screening, the values reported by VASP are often not recommended.
Another important detail concerns the implementation of the local LDA part in VASP. Literature [see Eqs. (3.10), (3.14), and (3.15) in Ref. [1]] suggests to use in the enhancement factor [math]\displaystyle{ F(z) }[/math] a position-independent variable [math]\displaystyle{ z=k_{\rm TF}/\bar{k}_{\rm F} }[/math] where [math]\displaystyle{ \bar{k}_{\rm F} }[/math] is as defined above but using the average density [math]\displaystyle{ \bar{n} }[/math] in the unit cell. However, implemented in VASP is a position-dependent variable [math]\displaystyle{ z({\bf r})=k_{\rm TF}/k_{\rm F}({\bf r}) }[/math], where [math]\displaystyle{ k_{\rm F}({\bf r})=(3\pi^2 n({\bf r}))^{1/3} }[/math] is the Fermi wave vector calculated with the local density [math]\displaystyle{ n({\bf r}) }[/math], while the constant [math]\displaystyle{ k_{\rm TF} }[/math] is set by HFSCREEN.
Related tags and articles
AEXX, BEXX, ALDAX, ALDAC, AGGAX, AGGAC, AMGGAX, AMGGAC, HFSCREEN, LHFCALC, LMODELHF, LTHOMAS, LRHFCALC, List of hybrid functionals, Downsampling of the Hartree-Fock operator, Coulomb singularity
References
- ↑ a b c A. Seidl, A. Görling, P. Vogl, J.A. Majewski, and M. Levy, Phys. Rev. B 53, 3764 (1996).
- ↑ J. Paier, R. Hirschl, M. Marsman, and G. Kresse, J. Chem. Phys. 122, 234102 (2005).
- ↑ J. P. Perdew, M. Ernzerhof, and K. Burke, J. Chem. Phys. 105, 9982 (1996).
- ↑ a b J. P. Perdew, K. Burke, and M. Ernzerhof, Phys. Rev. Lett., 77, 3865 (1996).
- ↑ P. J. Stephens, F. J. Devlin, C. F. Chabalowski, and M. J. Frisch, J. Phys. Chem. 98, 11623 (1994).
- ↑ A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A 38, 3098 (1988).
- ↑ C. Lee, W. Yang, and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B 37, 785 (1988).
- ↑ S. H. Vosko, L. Wilk, and M. Nusair, Can. J. Phys. 58, 1200 (1980).
- ↑ a b J. Heyd, G. E. Scuseria, and M. Ernzerhof, J. Chem. Phys. 118, 8207 (2003).
- ↑ a b J. Heyd and G. E. Scuseria, J. Chem. Phys. 121, 1187 (2004).
- ↑ a b J. Heyd, G. E. Scuseria, and M. Ernzerhof, J. Chem. Phys. 124, 219906 (2006).
- ↑ a b A. V. Krukau , O. A. Vydrov, A. F. Izmaylov, and G. E. Scuseria, J. Chem. Phys. 125, 224106 (2006).
- ↑ J. H. Skone, M. Govoni, and G. Galli, Nonempirical range-separated hybrid functionals for solids and molecules, Phys. Rev. B 93, 235106 (2016).
- ↑ W. Chen, G. Miceli, G.M. Rignanese, and A. Pasquarello, Nonempirical dielectric-dependent hybrid functional with range separation for semiconductors and insulators, Phys. Rev. Mater. 2, 073803 (2018).
- ↑ Z.H. Cui, Y.C. Wang, M.Y. Zhang, X. Xu, and H. Jiang, Doubly Screened Hybrid Functional: An Accurate First-Principles Approach for Both Narrow- and Wide-Gap Semiconductors J. Phys. Chem. Lett., 9, 2338-2345 (2018).
- ↑ H. Iikura, T. Tsuneda, T. Yanai, and K. Hirao, A long-range correction scheme for generalized-gradient-approximation exchange functionals, J. Chem. Phys. 115, 3540 (2001).
- ↑ I. C. Gerber and J. G. Ángyán, Hybrid functional with separated range, Chem. Phys. Lett. 415, 100 (2005).
- ↑ a b I. C. Gerber, J. G. Ángyán, M. Marsman, and G. Kresse, Range separated hybrid density functional with long-range Hartree-Fock exchange applied to solids, J. Chem. Phys. 127, 054101 (2007).
- ↑ a b D. M. Bylander and L. Kleinman, Phys. Rev. B 41, 7868 (1990).
- ↑ S. Picozzi, A. Continenza, R. Asahi, W. Mannstadt, A.J. Freeman, W. Wolf, E. Wimmer, and C.B. Geller, Phys. Rev. B 61, 4677 (2000).
