Category:Electron-phonon interactions: Difference between revisions

In many systems, it suffices to treat the electronic and vibrational degrees of freedom (phonons) separately, because electrons are much faster than the motion of nuclei. This treatment is approximate and can be corrected by including electron-phonon coupling. This entails the coupling of the two systems while still treating the two systems separately. In fact, electron-phonon scattering is the prevalent effect in a wide range of applications, such as the mobility of semiconductors or the conductivity of metals at room temperature.

The inclusion of the effects of the ionic degrees of freedom in the electronic structure is important in the determination of many physical observables such as the bandgap, spectral functions, electronic conductivity, Seebeck coefficient or electronic thermal conductivity, to name a few.

Overview

One can use different approaches to include electron-phonon coupling:

• statistically averaging observables during a molecular dynamics calculation,
• stochastic displacements approach, or
• using perturbation theory (available as of VASP 6.5.0).

In this page we outline the two later approaches, with their advantages and disadvantages for a range of applications . For a comprehensive overview of the theory of electron-phonon coupling, we recommend the review by F. Giustino ^[1].

Theory

There are a number of theory sections describing the stochastic displacements approach and many-body perturbation theory self-energy.

The renormalized bandgap is specifically covered for Monte Carlo and MBPT.

The chemical potential is important for calculating the electronic transport coefficients such as electrical conductivity, carrier mobility, and thermopower. More details about the theory behind these electronic transport coefficients is available in the theory page.

Calculations

For performing calculations, there are a series of pages covering: how acccumulators are used to efficiently reuse the electron-phonon matrix elements, electron-phonon potentials and generating the potentials from supercells.

The many-body perturbation theory (MBPT) approaches are run using ELPH_MODE and ELPH_DRIVER determines if the electron-phonon matrix elements are stored or used to calculate the self-energy. There are example calculations for calculating the zero-point renormalized (ZPR) bandgap using the stochastic displacements approach and many-body perturbation theory. There is also a brief overview for calculating transport properties. An important option for transport is for determining the approximation used for scattering lifetimes due to electron-phonon coupling, ELPH_SCATTERING_APPROX.

Stochastic displacements approach

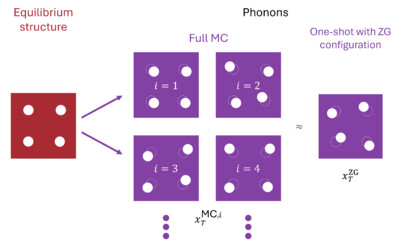
The stochastic approach allows obtaining the bandgap renormalization and an approximation of the electronic spectral function due to the ionic degrees of freedom under the static approximation using a supercell approach. This has the advantage that it can be easily implemented and used with different levels of theory to describe the electronic states, such as different exchange-correlation functionals or even the GW approximation. The disadvantage is that the approach does not include time-dependent or dynamical effects of the phonons (static approximation) and, hence, it does not provide transport properties (see perturbation theory).

To displace the atoms along a set of random or a single specially chosen direction ^[2], this approach requires the knowledge of the phonons on a supercell. The displacement length is determined by the temperature of the ionic system. The desired can be directly obtained by averaging over the set of randomly displaced supercells, or from the aforementioned special displacement pattern.

The theory of electron-phonon interactions from statistical sampling is covered elsewhere, as is a how to.

Many-body perturbation theory

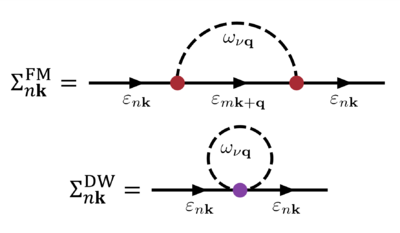
Another approach to include electron-phonon coupling employs the methods and language of many-body perturbation theory, where the coupling is included as a perturbation of the electronic or phononic states. In the case of the perturbation of the electronic states, we can access the bandgap renormalization as well as electronic transport coefficients with the inclusion of phonon scattering.

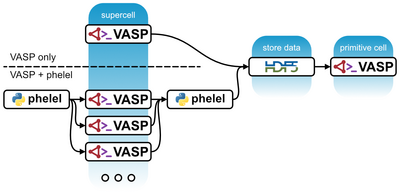
This approach entails computing the electron-phonon matrix element and the phonon-induced electron self-energy. Within the framework of density-functional theory, this requires the knowledge of the change of Kohn-Sham potential with an ionic perturbation as well as the initial and final electronic Kohn-Sham states. The electron-phonon potential must be generated from a supercell calculation, which is then used to calculate the phonon-induced electron self-energy and, thereby, the physical observables.

Electron-phonon potential from supercells

We obtain the derivatives of the Kohn-Sham potential with respect to the ionic displacements

[math]\displaystyle{ \partial_{I \alpha} V (\mathbf{r}) = \frac{\partial V(r)}{\partial R_{I\alpha}} }[/math]

with [math]\displaystyle{ I }[/math] the ion index and [math]\displaystyle{ \alpha }[/math] denoting the Cartesian direction in which it is displaced. The main output file is phelel_params.hdf5, which is required for computing the matrix elements in the next step.

• How to compute the electron-phonon potential from supercells

Physical observables (or electron-phonon matrix elements)

These physical observables include the zero-point renormalization (ZPR), and transport coefficients such as the electrical conductivity, carrier mobility, and thermopower and the ZT figure of merit. These electronic transport coefficients are derived from the electron-phonon matrix elements via the scattering lifetimes according to an approximation defined by ELPH_SCATTERING_APPROX, and Onsager coefficients, which depend on the chemical potential.

To compute the physical observables, the phonon-induced electron self-energy is computed in the primitive cell. The main tag that provides convenient defaults depending on the observable of interest is ELPH_MODE. The computation of the self-energy requires evaluating the electron-phonon matrix elements

[math]\displaystyle{ g_{mn \mathbf{k}, \nu \mathbf{q}} \equiv \langle \psi_{m \mathbf{k} - \mathbf{q}} | \partial_{\nu \mathbf{q}} V | \psi_{n \mathbf{k}} \rangle. }[/math]

By default, we avoid writing the matrix elements, because it is a huge data set which is distributed for optimal use of the computational resources.

For details on the setup and practical advice, we recommend reading

• Bandgap renormalization due to electron-phonon coupling
• Transport coefficients including electron-phonon scattering
• See the ELPH_DRIVER tag to obtain the electron-phonon matrix elements for further post-processing

The standard output of the electron-phonon code is organized using so-called electron-phonon accumulators. This increases the efficiency of the code by reusing the computed electron-phonon matrix elements. For details on how to interpret the output, consult the output section on the accumulators page.

Choosing the right approach

Both the (SA) as well as the (PA) have advantages and limitations. Depending on the application, there is often one approach that is much more suitable than the other. This section is dedicated to highlighting the differences and respective advantages between SA and PA so that choosing the correct approach becomes easier.

Likely the biggest deciding factor between SA and PA are the observables that can be calculated:

• To compute transport coefficients including electron-phonon scattering, the PA is the only possible choice. Transport calculations need to include time-dependent, i.e. dynamical, effects of the phonons. These effectively yield electronic quasiparticle lifetimes that influence properties such as the electronic conductivity [math]\displaystyle{ \sigma }[/math], the Seebeck coefficient [math]\displaystyle{ S }[/math] and the electronic contribution to the thermal conductivity [math]\displaystyle{ \kappa_e }[/math].

• The SA can calculate the renormalization of the fundamental bandgap of semiconductors and insulators, but not for metallic systems. Additionally it is difficult to infer the renormalization of the band structure at arbitrary k points in the primitive unit cell, as one would need a map of the states in the displaced supercell to the primitive cell that is not readily available and stated are heavily entangles. In comparison, the PA employs many-body perturbation theory to calculate entire band-structure renormalization, not just for gaped systems but also for metallic systems.

In materials that are strongly anharmonic, such as very soft materials with weakly bound atoms, the SA has a clear edge over PA. This is because the PA is limited by the harmonic approximation of phonons and only considers terms in the electron-phonon interaction up to second order in the atomic displacements. On the other hand, the SA computes the electron-phonon interaction implicitly during the electronic minimization procedure in the displaced geometry and is hence not limited to the harmonic approximation of phonons.

Furthermore, the SA can directly utilize higher-level exchange-correlation functionals such as METAGGA, hybrid functionals and beyond-DFT methods such as the GW approximation. While it is in principle possible to integrate these features also into the PA, this is currently not supported. Therefore, when the quasiparticle shifts due to electron-electron interactions become important, it is possible to use the PA method in combination with the GW approximation ^[3].

Another key difference is how PA and SA handle polar materials: In polar materials, longitudinal optical phonons can induce long-range electrostatic fields (Fröhlich interaction) that are difficult to capture in even very large supercells. The PA can deal with this via a special treatment of the dipole interaction that explicitly accounts for the missing long-range character in finite supercells. The SA, however, has no such correction scheme, which can be detrimental for strongly polar materials. In this case, one can only try to keep increasing the supercell size in hopes of arriving at a physically meaningful result.

References